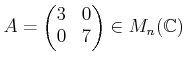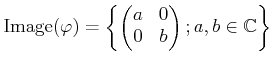Next: About this document ...
代数学演習 IB 問題 No.6

問題 6.2 (全部で1)
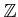
から
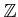
への環準同型
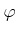
があったとする。
-
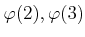 を求めよ。
を求めよ。
- 任意の
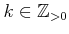 にたいして、
にたいして、
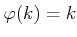 であることを示しなさい。
であることを示しなさい。
-
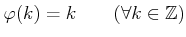 を示しなさい。
を示しなさい。
問題 6.4
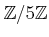
から
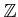
への環準同型は
存在するだろうか。存在する場合には全て挙げ、
存在しない場合はその理由をのべよ。
問題 6.5
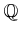
から
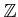
への環準同型は
存在するだろうか。存在する場合には全て挙げ、
存在しない場合はその理由をのべよ。
問題 6.6
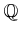
から
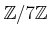
への環準同型は
存在するだろうか。存在する場合には全て挙げ、
存在しない場合はその理由をのべよ。
問題 6.7
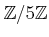
から
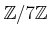
への環準同型は
存在するだろうか。存在する場合には全て挙げ、
存在しない場合はその理由をのべよ。
問題 6.9
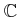
から
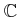
への準同型写像の例を二つ(以上)挙げなさい。
(二つはかなり簡単に見つかるが、三つめを挙げるのは超難問である。
それゆえ二つ答えるのが無難である。)
以下この演習では、とくに断らないで
![$ [?]_n$](img32.png) で
で 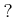 の
の
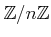 でのクラスを表すことがある。
文脈でわかると思うので、いちいち書かないが、注意していただきたい。
でのクラスを表すことがある。
文脈でわかると思うので、いちいち書かないが、注意していただきたい。
問題 6.10
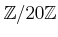
から
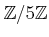
への写像
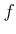
を
で定める。
このとき、
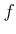
はうまく定義されていて、環準同型である
ことを示しなさい。
問題 6.11
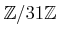
から
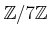
への写像
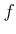
を
で定めたいが、
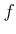
はうまく定義されていて、環準同型である
だろうか。理由をつけて答えなさい。
問題 6.12
体
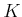
から 環
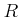
への準同型写像は
必ず単射であることを示しなさい。
問題 6.13
環準同型写像
![$ f:{\mbox{${\mathbb{Z}}$}}/18{\mbox{${\mathbb{Z}}$}}\ni [x]_{18}\mapsto [x]_6 \in {\mbox{${\mathbb{Z}}$}}/6{\mbox{${\mathbb{Z}}$}}$](img41.png)
を考える。
一行目に
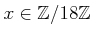
(18個), 二行目に
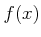
が並んだような表を作り、
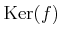
,
![$ f^{-1}([1]_6)$](img45.png)
,
![$ f^{-1}([2]_6)$](img46.png)
をそれぞれ求めなさい。
問題 6.14
環準同型写像
![$ f:{\mbox{${\mathbb{Z}}$}}/20{\mbox{${\mathbb{Z}}$}}\ni [x]_{20} \mapsto [x]_{4}\in {\mbox{${\mathbb{Z}}$}}/4{\mbox{${\mathbb{Z}}$}}$](img47.png)
を考える。
一行目に
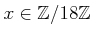
(18個), 二行目に
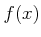
が並んだような表を作り、
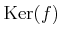
,
![$ f^{-1}([1]_6)$](img45.png)
,
![$ f^{-1}([2]_6)$](img46.png)
をそれぞれ求めなさい。
問題 6.15
行列
にたいして、
を
で定義する。
このとき、
-
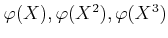 を求めなさい。
を求めなさい。
-
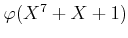 をもとめなさい。
をもとめなさい。
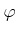 は環準同型であることを示しなさい。
は環準同型であることを示しなさい。
-
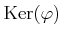 を求めなさい。
を求めなさい。
であることを証明しなさい。



Next: About this document ...
2011-11-14
![]()
![]() で
で ![]() の
の
![]() でのクラスを表すことがある。
文脈でわかると思うので、いちいち書かないが、注意していただきたい。
でのクラスを表すことがある。
文脈でわかると思うので、いちいち書かないが、注意していただきたい。