


Next: About this document ...
代数学演習 IB 問題 No.4

問題 4.1 (各1)
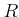
は単位元をもつ環であるとし、
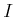
をそのイデアルとする。
このとき、
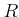 に同値関係
に同値関係 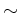 が、次のようにして決まることをしめしなさい。
が、次のようにして決まることをしめしなさい。
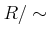 に、足し算を次のようにして入れる。
に、足し算を次のようにして入れる。
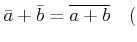
$?$ は $?$ の $&sim#sim;$ に関する
クラスを表す。
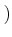
この足し算はうまく定義されていて、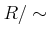 はこの足し算について可換群になる
ことをしめしなさい。
はこの足し算について可換群になる
ことをしめしなさい。
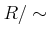 に、かけ算を次のようにして入れる。
に、かけ算を次のようにして入れる。
このかけ算はうまく定義されていて、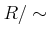 はこのかけ算について半群になる
ことを示しなさい。
はこのかけ算について半群になる
ことを示しなさい。
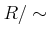 は上で定義された足し算、かけざんに関し環をなすことを示しなさい。
この環の単位元はなにですか?
は上で定義された足し算、かけざんに関し環をなすことを示しなさい。
この環の単位元はなにですか?
定義 4.1
上の補題の仮定のもとで、
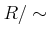
に上のような足し算、かけ算を入れて
環にしたものを
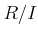
と書き、
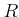
の
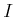
による剰余環と呼ぶ。
問題 4.4
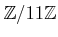
の元
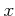
で
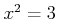
を満たすものをすべて求めなさい。
問題 4.5
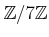
の元
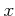
で
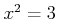
を満たすものをすべて求めなさい。
問題 4.6
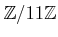
の元
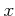
で
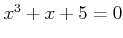
を満たすものをすべて求めなさい。
問題 4.7
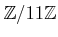
の元
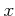
で
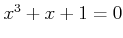
を満たすものをすべて求めなさい。
問題 4.8
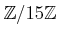
の元
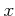
で
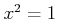
を満たすものを、全て挙げなさい。
問題 4.9
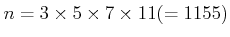
とする。
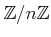
のなかで、
を満たすものを、全て挙げなさい。
(それで全部であることを証明すること。)
問題 4.10
を
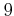
で割ったあまりはいくらだろうか?
できるだけ簡潔な理由をつけて(計算機を
用いることなく)答えなさい。
問題 4.11
を
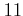
で割ったあまりはいくらだろうか?
できるだけ簡潔な理由をつけて(計算機を
用いることなく)答えなさい。
問題 4.12
を
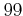
で割ったあまりはいくらだろうか?
できるだけ簡潔な理由をつけて(計算機を
用いることなく)答えなさい。
問題 4.13
次のことを正当化しなさい。
「
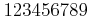
を
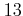
で割った余りは
を
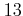
で割った余りとおなじである。
任意の9桁の数で同様のことができる。」
問題 4.14
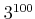
の下3桁を計算機を使わずに計算せよ。
問題 4.15
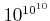
を
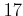
で割った余りを計算せよ。
(注意)
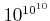 は
は
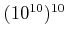 とは(当然のことながら)まるで異なる。
とは(当然のことながら)まるで異なる。



Next: About this document ...
2011-10-26
![]()
![]() は
は
![]() とは(当然のことながら)まるで異なる。
とは(当然のことながら)まるで異なる。