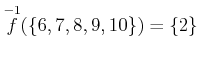- P の否定命題を「not を使わずに」書きなさい。(答のみで良い。)
- P と not P のうち、真であるのはどちらだろうか。真である方の 命題を明記し、それを証明しなさい。
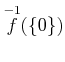 を求めよ。
を求めよ。
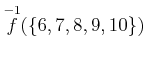 を求めよ。
を求めよ。
解答
16.1
(1) P の否定は
である。
(2) P のほうが真である。
[証明]
![]()
![]()
![]()
![]() を持ってくる。いま、
を持ってくる。いま、 ![]() と仮定すると、
と仮定すると、
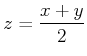
は
を満たす
(
![]() ここのところは、もう少し詳しく言えば
ここのところは、もう少し詳しく言えば
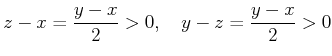
であるからである。)
16.2
(1)
 |
||
(2)
![]() における
における ![]() の値はそれぞれ
の値はそれぞれ
であり、
同様に、
ゆえに、