第9回目の主題 :
![]()
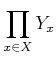
の元
と書く場合もある。
◎「ホテルヒルベルト」
一般に、 ![]() から
から ![]() への単射が存在することは、
への単射が存在することは、
![]() の元のほうが
の元のほうが ![]() の元よりも「少ない」ことを意味すると考えられる。
の元よりも「少ない」ことを意味すると考えられる。
![]() の各々の元を「人」、
の各々の元を「人」、![]() の各々の元を「ホテルの部屋」に例えると、
単射の存在は一人ひとりが別々の部屋に入れることを意味するからである。
ただし、無限集合においては、「多い」「少ない」の感覚は有限集合とは
少し異なる。
の各々の元を「ホテルの部屋」に例えると、
単射の存在は一人ひとりが別々の部屋に入れることを意味するからである。
ただし、無限集合においては、「多い」「少ない」の感覚は有限集合とは
少し異なる。
がなりたつ。
がなりたつ。
濃度の言葉(とベルンシュタインの定理)を用いると、次のことが分かる
写像の合成
で定義する。
である。また、任意の整数
一般に、実数 ![]() と整数
と整数 ![]() に対して、
に対して、
にも注意しておこう。昔は