第6回目の主題 :
![]()
正の実数 ![]() に対して、
に対して、
![]()
![]()
![]() ,
,
![]()
![]()
![]() とおく。
とおく。
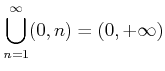
であることを示しなさい。
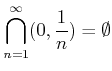
であることを示しなさい。
![$\displaystyle \bigcap_{\epsilon>0} (-\infty, 1+\epsilon) =(-\infty, 1]
$](img9.png)
であることを示しなさい。
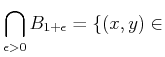
が成り立つことを示しなさい。
![]()
![]()
![]() にたいし、そのノルムを
にたいし、そのノルムを
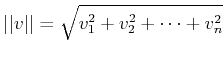
で定義する。このとき、
がなりたつ。(三角不等式。)
一般に、
![]()
![]()
![]() と
と ![]() に対して、
に対して、
(
が成り立つことを証明せよ。
![]()
![]() の部分集合
の部分集合 ![]() は
は
を満たすとき、(通常位相に関して)開集合であると呼ばれる。 開集合とは、「境界を含まない集合」ということの数学的な表現である。
「境界」という言葉自体も数学的に表現できるが、 ここではそこまでは踏み込まないことにする。