


Next: About this document ...
微分積分学概論AI要約 No.15

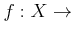
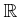 が
が 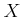 上で連続であるのは
上で連続であるのは
を満たすときに言うのであった。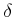 は
は
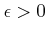 と
と 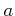 に依存して良いという
ことに注意する。
に依存して良いという
ことに注意する。
定義 15.1
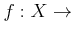
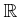
が
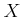
上で
一様連続であるとは、
を満たすときに言う。
一様連続性を言うためには、
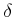 は
は 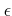 だけに依存し、
だけに依存し、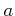 が
が 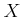 を動きまわっても
変わらないように取らなければならないという点に注意する。
を動きまわっても
変わらないように取らなければならないという点に注意する。
上の例題の 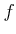 は任意の
は任意の 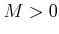 について、
について、![$ [-M,M]$](img18.png) において一様連続だが、
において一様連続だが、
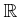 においては一様連続ではない。
このように一様連続性では定義域がどれであるかが大変大事である。
においては一様連続ではない。
このように一様連続性では定義域がどれであるかが大変大事である。
2011-07-29
![]()
![]()
![]() が
が ![]() 上で連続であるのは
上で連続であるのは
![]() は任意の
は任意の ![]() について、
について、![]() において一様連続だが、
において一様連続だが、
![]() においては一様連続ではない。
このように一様連続性では定義域がどれであるかが大変大事である。
においては一様連続ではない。
このように一様連続性では定義域がどれであるかが大変大事である。