微分積分学概論AI要約 No.6

第6回目の主題 :

定義 6.1   数列 $\{a_n\}$ が与えられているとする。このとき、 自然数の狭義増加列 $n_1<n_2<n_3<\dots$ を定めて、

$$\{a_{n_j} ; j=1,2,3,\dots\}=\{a_{n_k}\}_{k=1}^\infty =\{a_{n_1},a_{n_2},a_{n_3},\dots\}$$

で与えられるような数列を $\{a_n\}$ の部分列という。

次のグラフは $[0,1]$ の点を「ランダムに」選んできて作った数列の 折れ線グラフである。

(グラフは$n=100$ までしかないが このあとずっと続いていると想像して頂きたい。) このような数列は一般にはどの数にも収束しない。しかし、 「エエトコドリ」して収束する部分列を取り出すことはできる。

定理 6.2 (``定理5'')   [ボルツァノ・ワイエルシュトラス] 有界な数列は、収束する部分列を持つ。

位相空間論の言葉で言えば、上の定理は「実数の閉区間が点列コンパクトである」 ということを言っている。一生懸命勉強したい人には微分積分学と 位相空間論を並行して学習することをおすすめする。

定義に従って判定しようとすると、数列 $\{a_n\}$ が収束するか否かはその収束先 $\alpha$ の値を前もって知る必要がある。 実際の場面では $\alpha$ を知ることができないのがしばしばである。 有界な単調増加数列ならば、その上限を考えればよいが、 そうでないような数列に対してはどのようにして収束、発散を判定すれば 良いだろうか。それに答えるのがコーシー列の考え方である。

定義 6.3   数列 $\{a_n\}$ がコーシー列であるとは、

$$\forall \epsilon>0 \exists N \in {\mbox{${\mathbb{Z}}$}}_{>0} \forall n,m \geq N \quad \vert a_n-a_m\vert<\epsilon$$

がなりたつときに言う。

補題 6.4   ``定理6前半'' 実数の収束列はコーシー列である。

定理 6.5 (``定理6後半'')   コーシー列は収束列である。

問題 6.1   つぎの2つの問に答えなさい。

1. $\{\frac{1}{2^n}\}_{n=1}^\infty$ は収束することを示しなさい。
2. 数列 $\{a_n\}$ が
   $$\vert a_n-a_{n+1} \vert \leq \frac{1}{2^n}$$
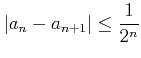
   を満たすとするとき、$\{a_n\}$ はコーシー列であることを示しなさい。

問題 6.2   実数列 $\{a_n\}$ であって、そのどの部分列も収束しないものの例を 挙げよ。 (理由も述べること。)

今回のように二問の問題がある場合にはどちらか一方だけ答えればよい。 但し、6.1 のように小問があるばあいにはすべての小問に答えること。

収束のイメージ。 上の図で言うと $\epsilon$ に対して $N=150$ 以降では $a_n$ が $c$ からみて上下 $\epsilon$ 未満の誤差に収まっている。

本講義の要約の紙(コレ)は http://www.math.kochi-u.ac.jp/docky/ からたどるとダウンロードできる。