


Next: Bibliography
Commutative algebra
Yoshifumi Tsuchimoto

Let us recall the universality of polynomial algebras.
As a corollary, we see:
LEMMA 08.3
Let 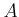 be a ring. Let
be a ring. Let 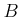 be an
be an 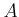 -algebra.
Let
-algebra.
Let 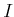 be a finitely generated ideal of
be a finitely generated ideal of 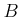 .
Let us denote by
.
Let us denote by
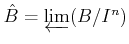 (respectively,
(respectively, 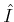 )
the completion of
)
the completion of 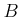 (respectively,
(respectively, 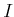 ) with respect to the
) with respect to the 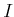 -adic
topology.
Then
-adic
topology.
Then 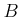 is
is 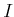 -smooth over
-smooth over 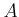 if and only
if
if and only
if 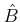 is
is 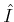 -smooth over
-smooth over 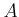 .
.
COROLLARY 08.4
Let 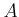 be a ring. Then
be a ring. Then
![$ A[[X_1,X_2,\dots, X_n]]$](img18.png) is
is 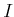 -smooth over
-smooth over
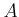 for
for
![$ I=\sum_{i=1}^n X_i A[[X_1,X_2,\dots, X_n]]$](img19.png) .
.
Note.
In general, ![$ A[[X]]$](img20.png) is not 0
-smooth over
is not 0
-smooth over 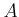 . See [1] and
the literatures cited there.
. See [1] and
the literatures cited there.
The following theorem says that the converse is true if the ring 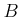 is 0
-smooth.
is 0
-smooth.



Next: Bibliography
2011-07-21
![]()
![]()
![]() is not 0
-smooth over
is not 0
-smooth over ![]() . See [1] and
the literatures cited there.
. See [1] and
the literatures cited there.