

![]()
解答編

![]()
に対して 準同型定理を適用すればわかる。
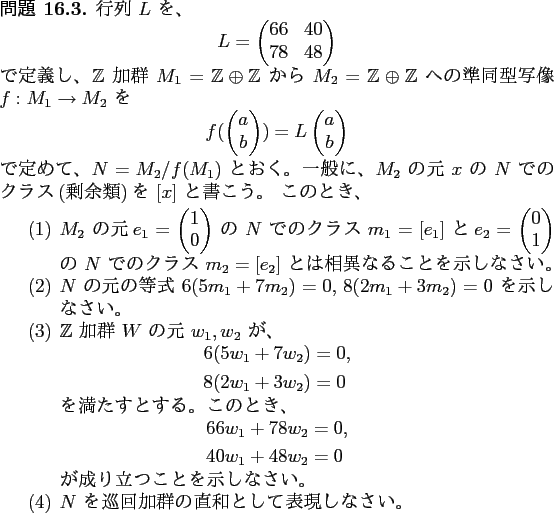
(1)
![]() であるとすると、
であるとすると、
![]() となる。
すなわち、ある
となる。
すなわち、ある
![]() が存在して、
が存在して、
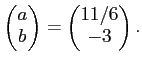
が(16.1)の唯一の解であることがわかる。すなわち、(16.1) を みたす整数
(2)
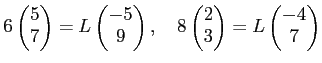
という関係式が存在するからである。
(3) 以下、行列による略記法を用いよう。わかりにくい場合には 適宜成分ごとに書いてみると良い。
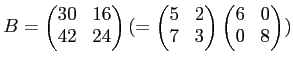
とおくと、
である。
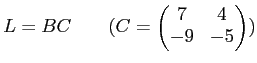
であるから、
(4)
![]() の 生成元として
の 生成元として ![]() ,
, ![]() を取ることができる。
その基本関係式は(行列記法を用いて略記すると)
を取ることができる。
その基本関係式は(行列記法を用いて略記すると)
である。 この関係式を簡単にしよう。 (2),(3) により、(あるいは、
と同値である。 他方
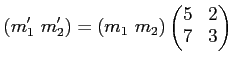
は基本変換の一つであり、上記関係式を
であることがわかる。 すなわち、
[本問のキーになるのは、(2)の解答のところの 等式をひとつにまとめた
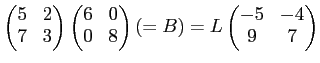
があって、この式に登場する
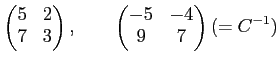
の二つの行列は整数係数の逆行列をもつという部分である。 ]