で定まるのであった。(例3.3)これにより、
今回は、行列のジョルダンの標準形について PID 上の加群の理論の立場から 概説しよう。つぎのような基本仮定を出発点とする。
基本仮定
|
で定まるのであった。(例3.3)これにより、 |
![]() は PID であるから、一般論(命題9.7)により、
次の命題が成り立つことがわかる。
は PID であるから、一般論(命題9.7)により、
次の命題が成り立つことがわかる。
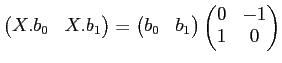
複素数体
![]() は代数的閉体であることが知られている。任意の体
は代数的閉体であることが知られている。任意の体 ![]() に対して、
それを含むような最小の代数的閉体
に対して、
それを含むような最小の代数的閉体 ![]() が存在することが
知られている。このような
が存在することが
知られている。このような ![]() のことを
のことを ![]() の代数的閉包
と呼ぶ。
の代数的閉包
と呼ぶ。
以下、![]() が代数的閉体のときを主に考える。このときには
が代数的閉体のときを主に考える。このときには ![]() 上の一変数
既約多項式は一次式に限るから、次のことがわかる。
上の一変数
既約多項式は一次式に限るから、次のことがわかる。
命題11.2のような基底を取れば、
![]() 上の
上の
![]() の作用の表現を得ることができるが、
の作用の表現を得ることができるが、![]() だけずらすことによって、
さらに良い基底を取ることもできる。
だけずらすことによって、
さらに良い基底を取ることもできる。
が取れる。
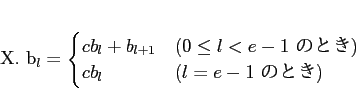
と書き下せる。行列で書くと
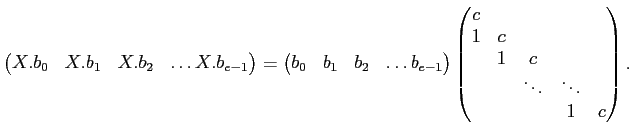
もしくは、基底の順番を取り換えて、
ただし
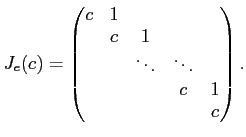
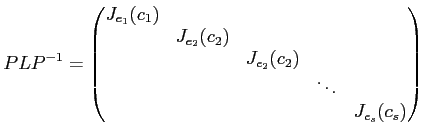
とジョルダン細胞の「直和」に分解される。
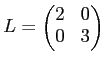
のとき、基本仮定のようにして