


Next: About this document ...
代数学II要約 No.4
第4回目の主題 :

「群の準同型定理」、「環の準同型定理」については既知であろう。
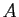 -加群の準同型定理も全く同様に定式化され、証明される。
それらのもとになるのは次の考え方である。
-加群の準同型定理も全く同様に定式化され、証明される。
それらのもとになるのは次の考え方である。
命題 4.1 (集合の準同型定理)
集合の間の写像
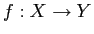
が与えられたとする。このとき、
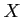 の上のクラスわけ(同値律)が、
の上のクラスわけ(同値律)が、
により定義される。
(このクラスわけによる 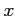 のクラスをここでは
のクラスをここでは ![$ [x]_f$](img7.png) と書こう。)
と書こう。)
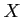 を上記のクラスわけによりクラスわけしたクラスの全体を
を上記のクラスわけによりクラスわけしたクラスの全体を 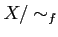 と
書くと、
と
書くと、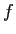 は
は
なる写像を誘導する。この写像は、(うまく定義されており、)全単射である。
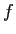 は次のように全射、全単射、単射の合成に分解される。
は次のように全射、全単射、単射の合成に分解される。
つぎのことに気をつけよう
- 単なる集合の場合に比べて加群の場合には「和、差、スカラー倍」という
構造を考慮に入れる必要がある。
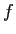 が加群の準同型のときには「
が加群の準同型のときには「 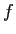 によるクラスわけ」は
で完全に制御される。
によるクラスわけ」は
で完全に制御される。
問題 4.1
を
![$ f([n]_{12})=[7 n]_{14}$](img24.png)
で「定義」する。
このとき
- これはうまく定義されていて、
-加群の準同型であることをしめしなさい。
- 次の対応表の下段を埋めなさい。(なるべく簡単な形にすること)
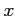
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
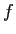 によって
はどのようにクラス分けされるか、「クラス分けの
表」を書き上げることによって示しなさい。
によって
はどのようにクラス分けされるか、「クラス分けの
表」を書き上げることによって示しなさい。



Next: About this document ...
2010-05-20
![]()
![]() -加群の準同型定理も全く同様に定式化され、証明される。
それらのもとになるのは次の考え方である。
-加群の準同型定理も全く同様に定式化され、証明される。
それらのもとになるのは次の考え方である。
![]() の像
の像 ![]() は
は ![]() の
の![]() -部分加群である。
-部分加群である。