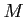 is a direct summand of free modules.
is a direct summand of free modules.
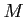 is projective
is projective
Yoshifumi Tsuchimoto
An ![]() -module
-module ![]() is said to be divisible if
for any
is said to be divisible if
for any
![]() , the multplication map
, the multplication map
is surjective.
An ![]() -module
-module ![]() is said to be divisible if
for any
is said to be divisible if
for any
![]() , the multplication map
, the multplication map
is epic.
For the proof of the proposition above, we need the followin lemmas.
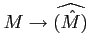 .
.
is