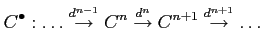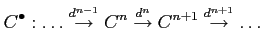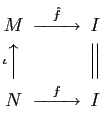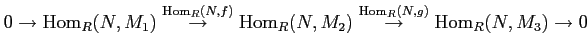Next: Bibliography
Cohomologies.
Yoshifumi Tsuchimoto
 We mainly follow the treatment in [1].
We mainly follow the treatment in [1].
DEFINITION 03.1
Let
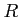
be a ring.
A
cochain complex of
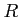
-modules
is a sequence of
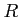
-modules
such that
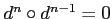
.
The
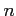
-th
cohomology of the cochain complex is defined to be the
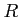
-module
Elements of
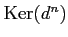
(respectively,
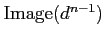
)
are often referred to as
cocycles (respectively,
coboundaries).
A bit of category theory:
DEFINITION 03.2
A
category
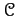
is a collection of the following data
- A collection
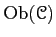 of objects of
of objects of
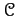 .
.
- For each pair of objects
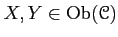 , a set
, a set
of morphisms.
- For each triple of objects
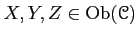 ,
a map(``composition (rule)'')
,
a map(``composition (rule)'')
satisfying the following axioms
-
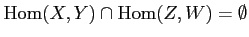 unless
unless
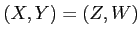 .
.
- (Existence of an identity) For any
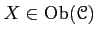 ,
there exists an element
,
there exists an element
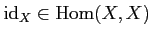 such that
such that
holds for any
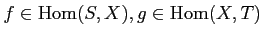 (
(
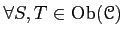 ).
).
- (Associativity)
For any objects
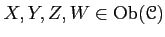 , and for any morphisms
, and for any morphisms
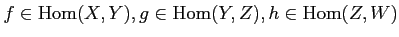 ,
we have
,
we have
Morphisms are the basic actor/actoress in category theory.
An additive category is a category in which one may ``add'' some morphisms.
DEFINITION 03.3
An additive category
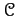
is said to be
abelian if it satisfies the
following axioms.
- A4-1.
- Every morphism
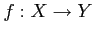 in
in
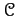 has a kernel
has a kernel
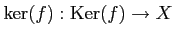 .
.
- A4-2.
- Every morphism
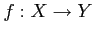 in
in
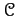 has a
cokernel
has a
cokernel
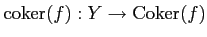 .
.
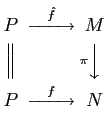
- A4-3.
- For any given morphism
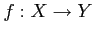 , we have
a suitably defined isomorphism
, we have
a suitably defined isomorphism
in
 .
More precisely,
.
More precisely, 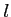 is a morphism which is defined by the following relations:
is a morphism which is defined by the following relations:
EXERCISE 03.1
Let
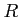
be a ring. Let
be an exact sequence of
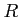
-modules.
Assume furthermore that
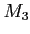
is projective.
Then show that
the sequence
is exact.



Next: Bibliography
2010-04-20