


Next: About this document ...
Cohomologies.
Yoshifumi Tsuchimoto
DEFINITION 01.1
A (unital associative)
ring is a set

equipped with two binary operations
(addition (``+'') and multiplication (``
'')) such that
the following axioms are satisfied.
- Ring1.
 is an additive group with respect to the addition.
is an additive group with respect to the addition.
- Ring2.
- distributive law holds. Namely, we have
- Ring3.
- The multiplcation is associative.
- Ring4.
 has a multiplicative unit.
has a multiplicative unit.
For any ring  , we denote by
, we denote by 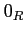 (respectively,
(respectively, 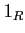 )
the zero element of
)
the zero element of  (respectively, the unit element of
(respectively, the unit element of  ).
Namely,
).
Namely, 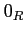 and
and 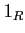 are elements of
are elements of  characterized by
the following rules.
characterized by
the following rules.
When no confusion arises, we omit the subscript `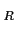 '
and write
'
and write 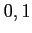 instead of
instead of 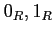 .
.
DEFINITION 01.4
An subset
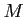
of an

-module
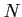
is said to be an
 -submodule
-submodule of
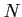
if
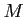
itself is an

-module and the inclusion map
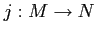
is an

-module homomorphism.
DEFINITION 01.5
Let
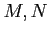
be modules over a ring

.
Then a map
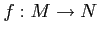
is called an
 -module homomorphism
-module homomorphism if
it is additive and preserves the

-action.
The set of all module homomorphisms from 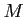 to
to 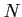 is denoted by
is denoted by
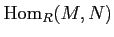 . It has an structure of an module in an obvious manner.
. It has an structure of an module in an obvious manner.
DEFINITION 01.6
An subset
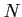
of an

-module
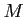
is said to be an
 -submodule
-submodule of
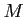
if
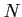
itself is an

-module and the inclusion map
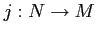
is an

-module homomorphism.
DEFINITION 01.7
Let

be a ring. Let
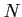
be an

-submodule of an

-module
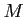
.
Then we may define the
quotient 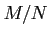
by
where the equivalence relation
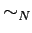
is defined as follows:
It may be shown that the quotient
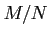
so defined is actually an

-module
and that the natural projection
is an

-module homomorphism.
DEFINITION 01.8
Let
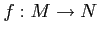
be an

-module homomorphism between

-modules.
Then we define its
kernel as follows.
The kernel and the image of an  -module homomorphism
-module homomorphism 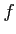 are
are  -modules.
-modules.
THEOREM 01.9
Let 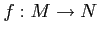 be an
be an  -module homomorphism between
-module homomorphism between  -modules.
Then
-modules.
Then
DEFINITION 01.10
Let

be a ring.
An ``sequence''
is said to be
an exact sequence of  -modules
-modules if the following conditions are satisfied
- Exact1.
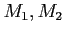 are
are  -modules.
-modules.
- Exact2.
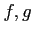 are
are  -module homomorphisms.
-module homomorphisms.
- Exact3.
-
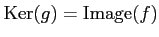 .
.
For any  -submodule
-submodule  of an
of an  -module
-module 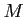 , we have the
following exact sequence.
, we have the
following exact sequence.
EXERCISE 01.1
Compute the following modules.
-
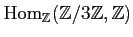 .
.
-
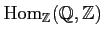 .
.
-
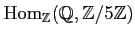 .
.



Next: About this document ...
2010-04-15
 is an additive group with respect to the addition.
is an additive group with respect to the addition.
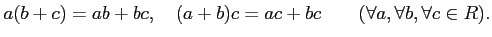
 has a multiplicative unit.
has a multiplicative unit.
![]() , we denote by
, we denote by ![]() (respectively,
(respectively, ![]() )
the zero element of
)
the zero element of ![]() (respectively, the unit element of
(respectively, the unit element of ![]() ).
Namely,
).
Namely, ![]() and
and ![]() are elements of
are elements of ![]() characterized by
the following rules.
characterized by
the following rules.
![]() to
to ![]() is denoted by
is denoted by
![]() . It has an structure of an module in an obvious manner.
. It has an structure of an module in an obvious manner.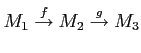
![]() -submodule
-submodule ![]() of an
of an ![]() -module
-module ![]() , we have the
following exact sequence.
, we have the
following exact sequence.