![]() 多変数関数の(リーマン)積分(5) 変数変換(つづき)。
多変数関数の(リーマン)積分(5) 変数変換(つづき)。
変数変換
![\includegraphics[scale=0.5]{14a.eps}](img13.png)
![\includegraphics[scale=0.5]{14b.eps}](img14.png)
小さな区間長方形
![]() 上では
上の変換はおおむね線形変換
上では
上の変換はおおむね線形変換
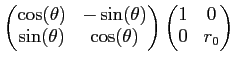
で近似され、よってその面積は変換によってほぼ
上の積分
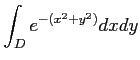
は長方形
上の積分
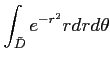
となる。これは容易に(累次積分により)積分されて答は
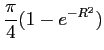
である。 このことは一変数の積分にも応用されて、
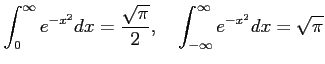
を得る。
変数変換の一次近似、Jacobian, 積分の変数変換が一堂に会する この辺が試験の問題になるであろう。やり方、考え方を 良く身につけておくこと。