![]() 多変数関数の(リーマン)積分(3) 変数変換。
多変数関数の(リーマン)積分(3) 変数変換。
次の定理は行列式の幾何学的意味を与える。
がなりたつ。
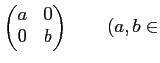 |
(対角行列) |
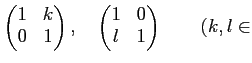 |
(「シフト」行列) |
![]()
![]() の開集合
の開集合 ![]() が与えられていて、
写像
が与えられていて、
写像
![]()
![]()
![]() が
が ![]() -級のとき、
-級のとき、
![]() は
は ![]() の各点
の各点 ![]() において
において
![]() で
近似されるのであった。したがって、
で
近似されるのであった。したがって、
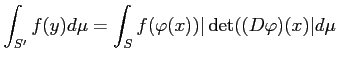
がなりたつ。
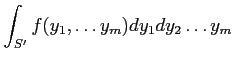 |
||
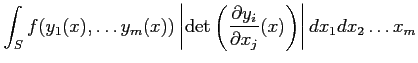 |
行列式
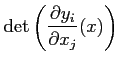
のことを変換のヤコビアン(Jacobian)と呼ぶ。
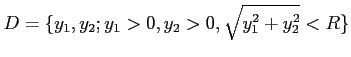
上の積分
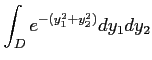
を計算せよ。
注意、定理の一般の状況にあわせるために、
変数名として
![]() をもちいたが、
上の問題はアカラサマに「極座標」への変換であるから
をもちいたが、
上の問題はアカラサマに「極座標」への変換であるから
上の積分
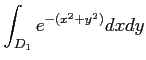
を変換