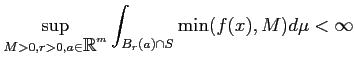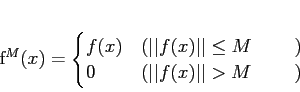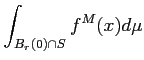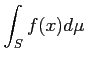Next: About this document ...
解析学 IA No.11要約
 多変数関数の(リーマン)積分(2)
多変数関数の(リーマン)積分(2)
定理 11.1
コンパクト集合 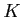 上の(実数値もしくはベクトル値)連続関数
上の(実数値もしくはベクトル値)連続関数 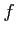 は一様連続である。
すなわち、
は一様連続である。
すなわち、
上の定理の系を述べるために、いくつか言葉を用意しよう。
定義 11.1
集合
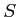
上の(実数値ベクトル値)関数
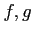
があるとする。
実数
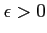
にたいして、
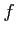
が
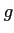
の
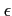 -近似
-近似であるとは、
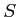
のどの点
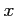
でも
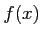
と
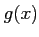
の距離が
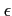
より小である
こと、すなわち
のときに言うことにする。
定義 11.2
測度確定の集合
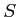
上の(実数値もしくはベクトル値)関数
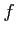
が
(この講義の意味で)
階段関数であるとは、
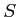
有限個の部分集合
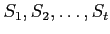
があって、つぎのことがなりたつときに言う。
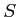 は
は
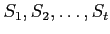 の互いに交わらない和集合である。
の互いに交わらない和集合である。
- 各
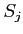 は測度確定である。
は測度確定である。
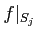 は定数値写像に等しい。
は定数値写像に等しい。
定義 11.3
測度確定の集合
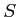
上の(実数値もしくはベクトル値)関数
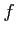
が
階段関数で一様近似可能であるとは、
任意の
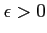
にたいして、
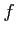
を
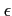
-近似するような階段関数
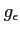
が存在するときに言う。
系 11.2
コンパクト集合 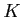 上の(実数値もしくはベクトル値)連続関数
上の(実数値もしくはベクトル値)連続関数 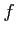 は
階段関数で一様近似可能である。
は
階段関数で一様近似可能である。
コンパクトかつ測度確定の集合 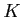 にたいして、
にたいして、
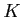 上のベクトル値関数
上のベクトル値関数 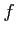 が階段関数で一様近似可能であれば、
が階段関数で一様近似可能であれば、
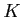 上の
上の 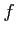 の積分
の積分
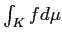 を前回の方針で定義することができる。
上の系により、
を前回の方針で定義することができる。
上の系により、 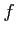 が連続ならば
が連続ならば 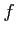 の積分が定まる。
の積分が定まる。
本格的には、階段関数について上の命題が正しいことを確認した上で、
連続性により積分を「階段関数で一様近似可能な関数」にまで拡張し、
そのように拡張した積分に対しても上の命題がなりたつことを示すのがよい。
同様の近似の議論により、つぎのことがわかる。
記述を簡単にするために、話を
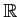
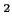 に限定するが、高次元でも
原理は同じである。
に限定するが、高次元でも
原理は同じである。
定理 11.4
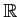
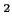 の部分集合
の部分集合 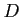 が、次のように連続関数
が、次のように連続関数 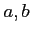 で定義されて
いたとする。(縦線集合)
で定義されて
いたとする。(縦線集合)
このとき、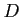 上の、階段関数で一様近似可能な関数
上の、階段関数で一様近似可能な関数 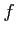 にたいして、
にたいして、
がなりたつ。
積分を考える集合 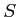 がコンパクトでない場合や、
がコンパクトでない場合や、
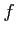 が有界でない場合はどうだろうか。
この場合は
が有界でない場合はどうだろうか。
この場合は 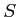 や
や 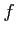 を適当に「切って」からその極限をとるのがよい。
そのようにして定義された積分を広義積分と呼ぶ。
詳細は教科書を参照のこと。
を適当に「切って」からその極限をとるのがよい。
そのようにして定義された積分を広義積分と呼ぶ。
詳細は教科書を参照のこと。
上の定義のように決められた積分は絶対収束する積分と呼ばれる。
積分が絶対収束する場合には、なにも上のように球体で切らなくても、
他の有界な領域で切っても「適切な」極限をとる限りは積分の値は
同じになる。



Next: About this document ...
2009-06-29
![]() 多変数関数の(リーマン)積分(2)
多変数関数の(リーマン)積分(2)
![]() にたいして、
にたいして、
![]() 上のベクトル値関数
上のベクトル値関数 ![]() が階段関数で一様近似可能であれば、
が階段関数で一様近似可能であれば、
![]() 上の
上の ![]() の積分
の積分
![]() を前回の方針で定義することができる。
上の系により、
を前回の方針で定義することができる。
上の系により、 ![]() が連続ならば
が連続ならば ![]() の積分が定まる。
の積分が定まる。
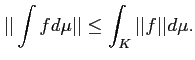
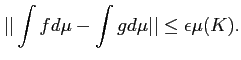
![]()
![]() に限定するが、高次元でも
原理は同じである。
に限定するが、高次元でも
原理は同じである。
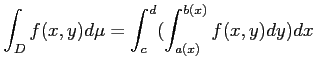
![]() がコンパクトでない場合や、
がコンパクトでない場合や、
![]() が有界でない場合はどうだろうか。
この場合は
が有界でない場合はどうだろうか。
この場合は ![]() や
や ![]() を適当に「切って」からその極限をとるのがよい。
そのようにして定義された積分を広義積分と呼ぶ。
詳細は教科書を参照のこと。
を適当に「切って」からその極限をとるのがよい。
そのようにして定義された積分を広義積分と呼ぶ。
詳細は教科書を参照のこと。