解析学 IA No.6要約

《積分による表示、多変数関数のテイラー展開。》

今回の話では、つぎのようなことをたびたび用いる。

補題 6.1   $[a,b]$ 上定義された(実数値もしくはベクトル値)連続関数 $f$ に対して

$$\vert\vert\int_a^b f(t)d t \vert\vert \leq \int_a^b \vert\vert f(t)\vert\vert d t$$

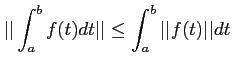
が成り立つ。

先週、定理5.3 の証明が残っていた。 次のような積分の計算が基本になる。 まずは微積分の基本定理から容易に従う一変数の場合。

$$f(x)=f(a)+(x-a)\int_0^1 f'(a+(x-a) t)$$

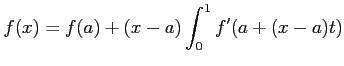
次は、それを用いた二変数の場合。

$$f(x,y) =f(a,y)+(x-a)\int_0^1 f_x(a+(x-a)t ,y) dt$$

$$= f(a,b) + (y-b)\int_0^1 f_y(a,b+(y-b)t )dt$$

$$+(x-a)\int_0^1 f_x(a+(x-a)t ,y) dt$$

ついでに、三変数だと以下のようになる。

$$f(x,y,z) = f(a,b,z) + (y-b)\int_0^1 f_y(a,b+(y-b)t,z )dt$$

$$+(x-a)\int_0^1 f_x(a+(x-a)t ,y,z) dt$$

$$= f(a,b,c) + (z-c) \int_0^1 f_z(a,b,c+(z-c)t )dt$$

$$+ (y-b)\int_0^1 f_y(a,b+(y-b)t,z )dt$$

$$+(x-a)\int_0^1 f_x(a+(x-a)t ,y,z) dt$$

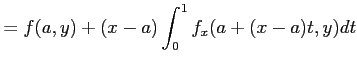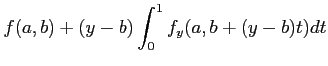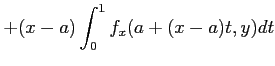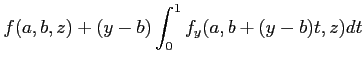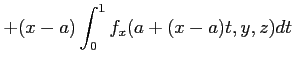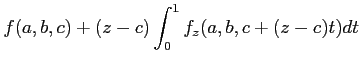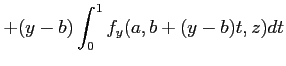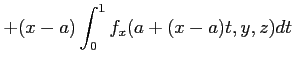以上は、偏微分は「軸方向の変化を記述する」ということからくる 制限の下で、苦労して $(a,b,c)$ から $(x,y,z)$ に近づいた式である。 一旦定理5.3 が確定した後は、$C^1$ 級関数は自動的に全微分可能である から、「まっすぐ」近づくほうがわかりやすい。

定理 6.1   $\mbox{${\mathbb{R}}$}$$^l$ の開集合 $U$ から $\mbox{${\mathbb{R}}$}$$^m$ への $C^1$ 級写像 $f$ について、 $U$ の点 $a$ と $x=a+h$ とを含む線分が $U$ に含まれているとするとき、等式

$$f(a+h)=f(a)+\int_0^1 Df(a+t h) \cdot h dt$$

が成り立つ。

《高階微分》

定義 6.1   $\mbox{${\mathbb{R}}$}$$^l$ の開集合 $U$ から $\mbox{${\mathbb{R}}$}$$^m$ への $C^1$ 級写像 $f$ について、

$$Df: U \ni a \mapsto Df(a) \in M_{m,l}($$$$\mbox{${\mathbb{R}}$}$$$$)$$

は、 $M_{m,l}($$\mbox{${\mathbb{R}}$}$$)$ を $\mbox{${\mathbb{R}}$}$$^{m l}$ と同一視することで、(全)微分可能性を 議論することができる。$D f$ の $x=a$ での微分を

$$D^2 f \vert _{x=a}$$

と書いて, $f$ の二階微分とよぶ。 つまり、 $D^2 f\vert _{x=a}$ は、 $\mbox{${\mathbb{R}}$}$$^l$ から $M_{m,l}($$\mbox{${\mathbb{R}}$}$$)$ への線型写像である。 $D^2 f\vert _{x=a}$ が各 $a\in U$ について存在して、連続であるとき、$f$ は $C^2$ 級であると呼ぶ。

命題 6.2   $\mbox{${\mathbb{R}}$}$$^l$ の開集合 $U$ 上定義された $C^2$ 級 写像 $f : U \to$   $\mbox{${\mathbb{R}}$}$$^m$ について、

$$f(a+h) = f(a)+ Df(a)\cdot h + \frac{1}{2}\int _0^1 \int _0^t D^2 (f(a+ts h)\cdot h)\cdot h d s d t$$

$$= f(a)+ Df(a)\cdot h + \frac{1}{2} (D^2f(a)\cdot h) \cdot h + o (\vert\vert h\vert\vert^2)$$

が成り立つ。

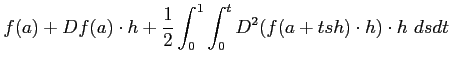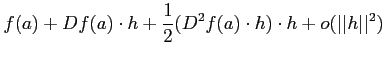微分と同様に高階微分も偏微分を用いて記述できる。

命題 6.3   $\mbox{${\mathbb{R}}$}$$^l$ の開集合 $U$ から $\mbox{${\mathbb{R}}$}$$^m$ への写像 $f$ が与えられているとする。 このとき、

1. $f$ が $C^2$ 級であることは、 各変数に関する一回偏導関数 $f_{x_1},f_{x_2},\dots ,f_{x_l}$ が 存在して、そのそれぞれが $C^1$ 級であることと同値である。
2. $f$ が $C^2$ 級である時、
   $$f_{{x_i} {x_j}}= f_{{x_j} {x_i}}$$
   がなりたつ。

(2)の証明では二変数の場合が本質的である。

$$f(x+h,y+k)-f(x,y+k)-f(x+h,y)+ f(x,y)$$

を二つの道筋で積分表示することになる。

※レポート問題

(期限：次の講義の終了時まで。)

問題 6.1   定理 6.1 に基づいて、 $f(x,y)=\sin(x y^2)$ について、

$$f(a+h,b+k)$$

の $h,k$ についての1次近似を求めなさい。すなわち、

$$f(a+h,b+k)= c_{00} + c_{10} h + c_{01} k + o(\vert\vert(h,k)\vert\vert)$$

なる実数 $c_{00},\dots, c_{01}$ を求めなさい。 できることならば剰余項の積分表示も求めてみること。