![]() 《合成関数の微分・連鎖律》
《合成関数の微分・連鎖律》
(全)微分を「一次近似」としてとらえると、 合成関数の微分は大変やさしい。
(``
全微分の行列成分は偏微分係数であったことを思い出すと、 次の系が得られる。
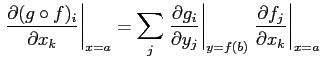
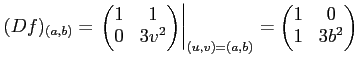 |
||
他方で、
であるから、
であって、簡単な行列算により、この場合に定理が実際に正しいことを 確かめられる。
変数の数 ![]() を変えて、上の系をいろいろ書き換えてみると良い。
``連鎖律''の感じが掴めるだろう。連鎖律は、変数変換を考える際に特に重要になる。
を変えて、上の系をいろいろ書き換えてみると良い。
``連鎖律''の感じが掴めるだろう。連鎖律は、変数変換を考える際に特に重要になる。
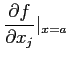
を
上の定義では、![]() としてはベクトル値を許して記述した。
下の定義でも
としてはベクトル値を許して記述した。
下の定義でも ![]() をベクトルのままで扱っても良いのであるが、
あえて成分で書いておくことにする。
をベクトルのままで扱っても良いのであるが、
あえて成分で書いておくことにする。
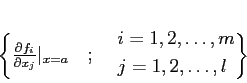
が存在して、しかも
上の定義は、確かめやすいが、偏微分を用いているので 「偏った」感じである。
証明には次の補題を(連続して)用いると良い。
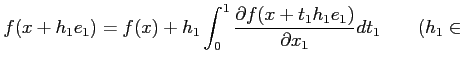
がなりたつ。ここに、
オット、次の定理も必要になる。証明は位相空間論の講義を参照のこと
※レポート問題
(期限:次の講義の終了時まで。)