解析学 IA No.3要約

《多変数関数の連続性と極限(2)》 「写像」と「関数」は同じ意味の言葉ではあるが、ニュアンスとしては 「関数」といえば値集合として数集合のみを許すことが多い。 今日はそんな「関数」に限らずもっと一般の「写像」の連続性も 一緒に議論しよう。詳しくは位相空間論で勉強するはずである。

定義 3.1   $\mbox{${\mathbb{R}}$}$$^n$ の部分集合 $S$ から $\mbox{${\mathbb{R}}$}$$^m$ の部分集合 $T$ への写像 $f$ が 点 $P\in S$ で連続であるとは、

$$\forall \epsilon \in$$   $$\mbox{${\mathbb{R}}$}$$$$_{>0} \exists \delta \in$$$$\mbox{${\mathbb{R}}$}$$$$_{>0} \left ( Q\in S\cap B_\delta(P) \implies d(f(Q),f(P))<\epsilon \right )$$

を満たすときに言う。

$f$ が $S$ のどの点でも連続であるとき、$f$ は連続であるという。

$d(f(Q),f(P))<\epsilon$ の部分は 「 $f(Q)\in B_\epsilon (f(P))$ 」と言い代えてももちろんよい。 「連続性」という解析学的なことがらが「球の位置関係」という幾何学的なことがらに 翻訳されていることに注意。

実際の関数の連続性は、基本的な関数の連続性を組み合わせてだすことがおおい。 基本的な関数自身の連続性はとなると、 これは結局上の定義に戻って証明することになる。

補題 3.1   次の各写像は連続である。

1. $f_+:$   $\mbox{${\mathbb{R}}$}$$^2 \ni (x,y)\mapsto x+y \in$   $\mbox{${\mathbb{R}}$}$
2. $f_-:$   $\mbox{${\mathbb{R}}$}$$^2 \ni (x,y)\mapsto x-y \in$   $\mbox{${\mathbb{R}}$}$
3. $f_{\times}:$   $\mbox{${\mathbb{R}}$}$$^2 \ni (x,y)\mapsto x y \in$   $\mbox{${\mathbb{R}}$}$
4. $\operatorname{inv}:$   $\mbox{${\mathbb{R}}$}$$\setminus \{0\} \ni x \mapsto x^{-1} \in$   $\mbox{${\mathbb{R}}$}$

補題 3.2   集合 $S \subset$   $\mbox{${\mathbb{R}}$}$$^l$ , $T \subset$   $\mbox{${\mathbb{R}}$}$$^m$ , $U \subset$   $\mbox{${\mathbb{R}}$}$$^n$ と 写像 $f: S\to T$ , $g: T\to U$ が与えられているとする。 $f$ が $P\in S$ で連続で、かつ $g$ が $f(P)\in T$ で連続ならば、 合成写像 $g\circ f$ も $P$ で連続である。とくに、連続写像の合成写像は 連続である。

連続写像を組み合わせて新しい写像を作るためには、 幾つかの「退屈な写像」(包含写像、射影など) について連続性を言わなければならない。 ここでそれをやると二度手間になってしまううえに、 位相空間の知識なしには中途半端にしかできないので、 それらはおとなしく位相空間論に任せよう。

◎ ランダウの $o$ .

定義 3.2   $\mbox{${\mathbb{R}}$}$$^n$ の部分集合 $X$ 上の関数 $a,b$ にたいして、

$$\forall \epsilon>0 \exists r>0 \quad( Q\in B_r(P)\cap X \implies \vert a(Q)\vert\leq \epsilon \vert b(Q)\vert)$$

が成り立つとき、

$$a(Q)=o(b(Q))$$

と書いて、$a$ は $b$ に比べて無視できる(ほど小さい)という。

上の定義の式は、ほぼ、

$$\lim_{Q \to P} \left\vert \frac{a(Q)}{b(Q)} \right \vert\to 0$$

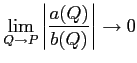
と同値である。ただ、$b=0$ の点で困るから、上の形にしてあるのである。

上の記法を用いると、$f$ が $P$ で連続であることは、

$$f(Q)=f(P)+o(1)$$

と同値である。

※レポート問題

(期限：次の講義の終了時まで。)

問題 3.1   写像 $f:$$\mbox{${\mathbb{R}}$}$$^2 \ni (x,y) \to (x^2, x^3+y^3) \in$   $\mbox{${\mathbb{R}}$}$$^2$ が 連続であることを示しなさい。