![]()
がなりたつときにいう。
極限の定義により、上の定義は次のように言い換えられる。
(☆)
![]()
上の定義で、 ![]() は
は ![]() と
と ![]() の距離、
の距離、
![]() は
は ![]() と
と
![]() の距離であることに注意する。上の定理による連続性の「定義」は
多変数関数や、距離空間のあいだの写像の連続性の定義に
そのまま一般化することができる。
の距離であることに注意する。上の定理による連続性の「定義」は
多変数関数や、距離空間のあいだの写像の連続性の定義に
そのまま一般化することができる。
上の定理は「定理」ではあるが、
連続性の定義における ``![]() '' の「例外的な扱い」を取り除いてむしろ
自然な形をしている。そこでこの講義ではもっぱら連続性を確かめるには
上の定理の(☆)で判定することにする。
'' の「例外的な扱い」を取り除いてむしろ
自然な形をしている。そこでこの講義ではもっぱら連続性を確かめるには
上の定理の(☆)で判定することにする。
を満たす正の数
を満たす正の数
(☆)の否定、すなわち、 「![]() が
が ![]() で連続でない」ことは、
次のように書き表すことができる。
で連続でない」ことは、
次のように書き表すことができる。
(★)
![]() かつ
かつ ![]()
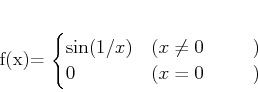
で定義するとき、
問題7.1 解答解説。
・ まず補題7.2, 定理7.3 すなわち、
「![]() がある数
がある数 ![]() に収束するということと、
に収束するということと、
![]() がコーシー列であるということは同値である」
を用いて解答するのを初級編としておいておけば良かったかも知れない。
がコーシー列であるということは同値である」
を用いて解答するのを初級編としておいておけば良かったかも知れない。
・
二重矢印 A ![]() B は「AならばいつでもBが成り立つ」の意味にしか使わない。
B は「AならばいつでもBが成り立つ」の意味にしか使わない。
◎ 状況をできるだけ具体的にイメージすることが解答への近道である。 そのためにはいくつか例を挙げてみるのも良い。 (ただし、例だけでは証明にはならないことも知っておくこと。)
問題7.1(1)の解答(初級編)。
![]() はコーシー列なので、ある実数
はコーシー列なので、ある実数 ![]() に収束する。(定理7.3)
ところが、仮定により、
に収束する。(定理7.3)
ところが、仮定により、![]() であることがわかる。
であることがわかる。
「収束の定義にでて来る ![]() 」として
」として ![]() をとると、
をとると、
がわかる。この
すなわち、
問題7.1(1)の解答。背理法で,結論の否定、すなわち
| (※) |
| (あ) |
上の式(※)の ![]() として
として
![]() ,
, ![]() として
として ![]() をとることにより、
ある
をとることにより、
ある ![]() が存在して、
が存在して、
| (い) |
が結論される。つまり、
ところが、仮定で、![]() は 0
に収束しないとしたわけだから、これは
矛盾である。
は 0
に収束しないとしたわけだから、これは
矛盾である。 ![]()
問題7.1 (2) の解答。
(まず始めに ![]() をつくることが肝要。)
をつくることが肝要。)
(1)のような ![]() を一つ選んで
を一つ選んで
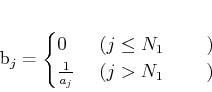
と定義する。 任意の
となる。すなわち、