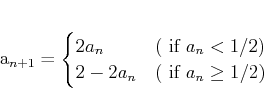Next: About this document ...
微分積分学概論AI要約 No.6

定理 6.1 (``定理1.6''[区間縮小法])
閉区間の列
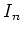
について、
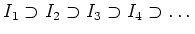
がなりたつとする。このとき、
さらに、
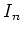
の長さを
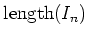
と書くとき、
がなりたつならば、
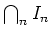
はただ一点のみからなる。
定義 6.2
数列
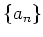
が与えられているとする。このとき、
自然数の狭義増加列
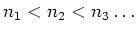
を定めて、
で与えられるような数列を
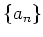
の部分列という。
(教科書の 1.2.6 は少し書き間違いがあるので注意。但し第3刷以降は直っている。)
例えば
や
(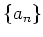 のうち素数番目のものをとりだしたもの),
のうち素数番目のものをとりだしたもの),
などはすべて 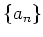 の部分列である。
の部分列である。
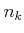 が狭義増加列であることから、
が狭義増加列であることから、 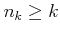 が全ての
が全ての 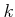 に
ついて成り立つ。このことから、直ちに次のことが従う。
に
ついて成り立つ。このことから、直ちに次のことが従う。
補題 6.3
数列
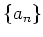
が
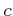
に収束するならば、その任意の部分列
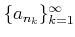
も
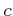
に収束する。
定理 6.4 (``定理1.9'')
[ボルツァノ・ワイエルシュトラス]
有界な数列は、収束する部分列を持つ。
例えば、問題2.1 の数列はそれ自体は収束しないが、収束する部分列を
もつ。実際、
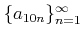 は
は 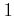 に収束するし、
に収束するし、
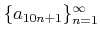 は 0
に収束する。
は 0
に収束する。
問題 6.1
補題
6.3を
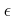
-
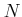
法を用いて証明せよ。
問題 6.2
数列
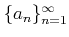
を、
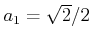
かつ
で定義する。このとき、
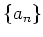
は収束する部分列を持つことを
(今日証明した定理のうちのどれかを用いて)証明しなさい。
2009-05-26
![]()
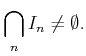
![]() が狭義増加列であることから、
が狭義増加列であることから、 ![]() が全ての
が全ての ![]() に
ついて成り立つ。このことから、直ちに次のことが従う。
に
ついて成り立つ。このことから、直ちに次のことが従う。
![]() は
は ![]() に収束するし、
に収束するし、
![]() は 0
に収束する。
は 0
に収束する。