


Next: About this document ...
Categories, abelian categories and cohomologies.
Yoshifumi Tsuchimoto
Let us denote by
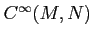 the set of all differentiable maps from
the set of all differentiable maps from
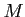 to
to 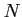 .
A so-called ``de Rham cohomology'' of
.
A so-called ``de Rham cohomology'' of 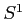 is computed as a cohomology of a
complex
is computed as a cohomology of a
complex
We see that:
Actually,
the dimension of the 0
-th cohomology
is related to a number of the connected
component of 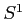 .
The dimension of the
.
The dimension of the 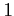 -st cohomology
is related to a number of the `hole'
of
-st cohomology
is related to a number of the `hole'
of 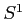 .
Cohomology is then a good tool to obtain numbers (``invariants'')
of geometric objects.
.
Cohomology is then a good tool to obtain numbers (``invariants'')
of geometric objects.
Cohomology also arises as ``obstructions''. Indeed, the de Rham cohomology
of the 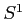 tells us a hint about ``which functions are integrable'', etc.
tells us a hint about ``which functions are integrable'', etc.
In this talk we give a definition and explain some basic properties of
cohomologies. But before that, we first deal with some category theory.
DEFINITION 01.1
A
category
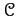
is a collection of the following data
- A collection
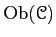 of objects of
of objects of
 .
.
- For each pair of objects
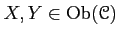 , a set
, a set
of morphisms.
- For each triple of objects
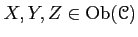 ,
a map(``composition (rule)'')
,
a map(``composition (rule)'')
satisfying the following axioms
-
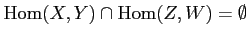 unless
unless
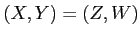 .
.
- (Existence of an identity) For any
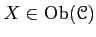 ,
there exists an element
,
there exists an element
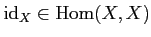 such that
such that
holds for any
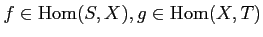 (
(
 ).
).
- (Associativity)
For any objects
 , and for any morphisms
, and for any morphisms
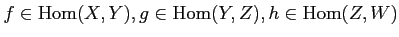 ,
we have
,
we have
LEMMA 01.3
Let 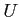 be an universe. Then the following statements hold.
be an universe. Then the following statements hold.
- If
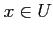 , then
, then
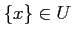 .
.
- If
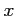 is a subset of
is a subset of 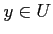 , then
, then 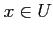 .
.
- If
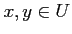 , then the ordered pair
, then the ordered pair
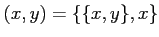 is in
is in 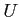 .
.
- If
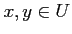 , then
, then 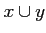 and
and 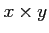 are in
are in 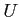 .
.
- If
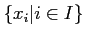 is a family of elements of
is a family of elements of 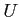 indexed
by an element
indexed
by an element 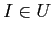 , then we have
, then we have
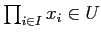 .
.
In this text we always assume the following.
For any set 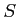 , there always exists a universe
, there always exists a universe 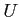 such that
such that 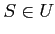 .
.
EXERCISE 01.1
Let us put
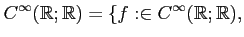
support of $f$ is compact
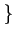
Then:
- Compute the cohomology group of the following complex.
- Compute the cohomology group of the following complex.



Next: About this document ...
2009-05-28
![]() the set of all differentiable maps from
the set of all differentiable maps from
![]() to
to ![]() .
A so-called ``de Rham cohomology'' of
.
A so-called ``de Rham cohomology'' of ![]() is computed as a cohomology of a
complex
is computed as a cohomology of a
complex
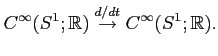
![]() tells us a hint about ``which functions are integrable'', etc.
tells us a hint about ``which functions are integrable'', etc.
![]() , there always exists a universe
, there always exists a universe ![]() such that
such that ![]() .
.