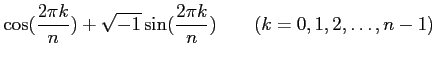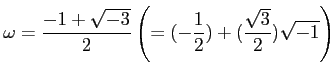Next: About this document ...
複素数と論理(学問基礎数学コース演習) No.4

前回までに、
任意の複素数複素数  にたいして、
にたいして、
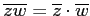 がなりたつ
がなりたつ
ということを証明した。
これは、
を全てまとめて証明したことと同じである。このように、
文字を用いていろいろな場合を
ひっくるめて証明してしまうと効率的に議論を運ぶことができる。
「任意の複素数 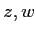 に対して」ということを式で表現するためには
に対して」ということを式で表現するためには
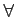 という記号をもちいて、
という記号をもちいて、
とか、
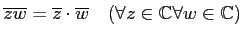 |
(☆) |
と書く。
これが正しいということは、「水の洩れるような穴がない」すなわち、
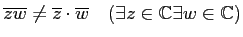 |
(★) |
のようなことが起こらない、ということである。
(★) と (☆) は、互いに一方の否定である。相手が間違っている
ということを示すには相手の主張の否定を証明することになる。
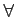 と
と 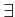 の順番(変数の登場順序)にも注意しよう。
の順番(変数の登場順序)にも注意しよう。
は正しい命題であるが、
はまったく正しくない命題である。
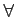 や
や 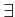 を含むような命題の否定命題を作るのは
たいへん簡単な規則があることにも注意しよう。
を含むような命題の否定命題を作るのは
たいへん簡単な規則があることにも注意しよう。
たとえば、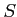 は数の集合であるとして、
は数の集合であるとして、
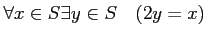 |
(AS) |
の否定は
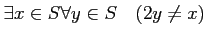 |
(BS) |
であることを、確かめて頂きたい。
例題 4.1
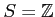
のときと
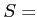
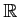
のときのそれぞれに対して、(AS) と (BS)
のどちらが正しいか、考えてみなさい。
定義 4.1
0
でない複素数
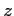
と、実軸の正の部分のなす角を
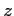
の
偏角といい、
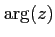
で書き表す。
偏角は一意には定まらない、ということに注意しよう。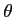 が
が 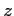 の
偏角なら、
の
偏角なら、
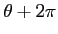 もそうである。
すなわち、
もそうである。
すなわち、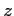 の偏角の全体は
の偏角の全体は
という集合をなすことが分かる。
そこで、偏角は
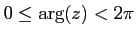 の範囲で選ぶ
(もしくは
の範囲で選ぶ
(もしくは
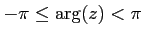 の範囲で選ぶ)
ということが良く行われるが、これはいつもそうしなければならない
というわけではない。
の範囲で選ぶ)
ということが良く行われるが、これはいつもそうしなければならない
というわけではない。
定理 4.1
複素数 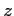 ,
, 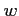 に対して、
に対して、
-
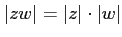
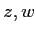 がどちらも 0
でないとき、
がどちらも 0
でないとき、
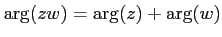
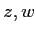 がどちらも 0
でないとき、
がどちらも 0
でないとき、
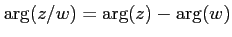
が成り立つ。
補題 4.1
偏角が 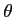 であるような複素数
であるような複素数 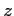 は
は
と書ける。(これを 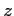 の 極表示 という。)
の 極表示 という。)
とくに、
定理 4.2
任意の正の整数 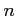 にたいして、
にたいして、
をみたす複素数がちょうど 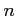 個あって、それらは
個あって、それらは
である。これらは 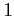 の
の 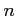 乗根と呼ばれる。
乗根と呼ばれる。
問題 4.1
複素数平面
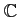
上にあなたの好きな一点
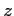
(ただし、0
や
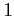
とは異なるもの)を
とり、
0
,
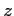
,
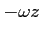
をプロットして線分で結んでみなさい。
どんな図形ができるでしょうか。
ただし、
とします。



Next: About this document ...
2009-01-27
![]()
![]() にたいして、
にたいして、
![]() がなりたつ
がなりたつ
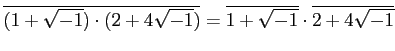
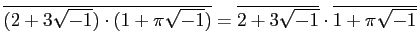
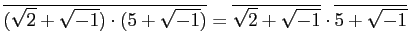
![]() と
と ![]() の順番(変数の登場順序)にも注意しよう。
の順番(変数の登場順序)にも注意しよう。
![]() や
や ![]() を含むような命題の否定命題を作るのは
たいへん簡単な規則があることにも注意しよう。
を含むような命題の否定命題を作るのは
たいへん簡単な規則があることにも注意しよう。
![]() は数の集合であるとして、
は数の集合であるとして、
![]() が
が ![]() の
偏角なら、
の
偏角なら、
![]() もそうである。
すなわち、
もそうである。
すなわち、![]() の偏角の全体は
の偏角の全体は