![]()
環 ![]() に対して、その元を成分にもつ行列を考えることができ、
通常の意味の和、差、積が(サイズがあっているという条件のもとで)
定義されて、一年生で習う線形代数のかなりの部分がそのまま
正しい。
に対して、その元を成分にもつ行列を考えることができ、
通常の意味の和、差、積が(サイズがあっているという条件のもとで)
定義されて、一年生で習う線形代数のかなりの部分がそのまま
正しい。
とおくと、これは(可換ではない)環である。 その単位元は
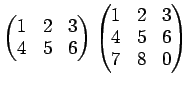
を計算し、できるだけ簡単な形、すなわち各成分の絶対値が 14以下の整数によって表されている形になるように直しなさい。
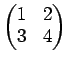
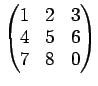
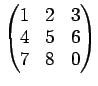
が成り立つことを証明しなさい。
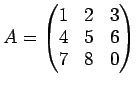
の逆行列は存在するだろうか。 行列式の乗法性
に基づいて答えなさい。
をみたす行列
を満たすものの例を挙げなさい。 (かなり難問である。
が成り立つことを証明しなさい。