![]()
がなりたつときにいう。
極限の定義により、上の定義は次のように言い換えられる。
(☆)
![]()
上の定義で、 ![]() は
は ![]() と
と ![]() の距離、
の距離、
![]() は
は ![]() と
と
![]() の距離であることに注意する。上の定理による連続性の「定義」は
多変数関数や、距離空間のあいだの写像の連続性の定義に
そのまま一般化することができる。
の距離であることに注意する。上の定理による連続性の「定義」は
多変数関数や、距離空間のあいだの写像の連続性の定義に
そのまま一般化することができる。
上の定理は「定理」ではあるが、
連続性の定義における ``![]() '' の「例外的な扱い」を取り除いてむしろ
自然な形をしている。そこでこの講義ではもっぱら連続性を確かめるには
上の定理の(☆)で判定することにする。
'' の「例外的な扱い」を取り除いてむしろ
自然な形をしている。そこでこの講義ではもっぱら連続性を確かめるには
上の定理の(☆)で判定することにする。
を満たす正の数
を満たす正の数
◎
![]() の否定。
の否定。
一般に、
したがって、(☆)の否定、すなわち、 「![]() が
が ![]() で連続でない」ことは、
次のように書き表すことができる。
で連続でない」ことは、
次のように書き表すことができる。
(★)
![]() かつ
かつ ![]()
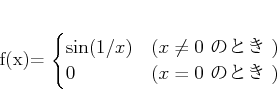
で定義するとき、