


Next: About this document ...
微分積分学概論AI要約 No.9

定理 9.1 (``教科書定理1.9'')
3つの
関数
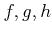
が、 実数
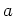
を含む区間
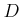
で定義されており、
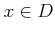
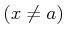
で、
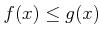
とする。このとき、
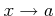 のときの
のときの 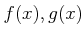 の極限がともに存在すれば、
の極限がともに存在すれば、
-
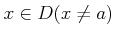 の範囲で、
の範囲で、
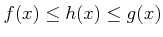 であって、
なおかつ
であって、
なおかつ
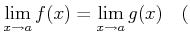
この等しい値を $A$ とおく
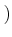
がなりたつとすると、 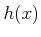 も
も 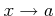 のときの極限が存在して、
のときの極限が存在して、
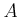 に等しい。
に等しい。
定理 9.2
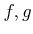
が
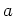
の近くで定義されており、
がそれぞれ存在するとする。このとき、
-
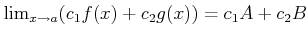 . (但し
. (但し
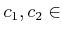
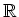 .)
.)
-
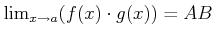 .
.
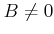 のとき、ある正の実数
のとき、ある正の実数 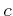 が存在して、
が存在して、 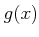 は
は
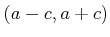 で(定義されてなおかつ) 0
以外の値をとり、
で(定義されてなおかつ) 0
以外の値をとり、
問題 9.1
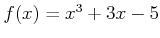
とおく。このとき、正の実数
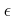
にたいして、
をみたすような正の数
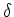
の例あげて、実際それを確かめなさい。
命題 9.3
関数
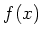
が
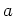
の近くで定義されており、
がなりたつとする。
このとき、点列
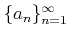
が
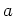
に収束すれば、
である。
命題 9.4
関数
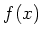
が
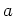
を含む開区間
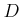
上で定義されており、ある実数
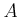
にたいして
「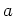 に収束する
に収束する 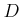 内の任意の数列
内の任意の数列
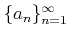 にたいして、
にたいして、
がなりたつ。」
をみたせば、
である。
2008-06-18
![]()
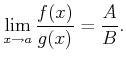
![]() に収束する
に収束する ![]() 内の任意の数列
内の任意の数列
![]() にたいして、
にたいして、