


: この文書について...
日本語技法 No.5
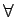 と
と 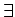 (その2)
(その2)
を証明するには、全ての 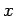 について一斉にチェックする必要がある。
(したがって、一般には何らかの巧妙な「多くのモノをさばく」テクニックが
必要になる。) について一斉にチェックする必要がある。
(したがって、一般には何らかの巧妙な「多くのモノをさばく」テクニックが
必要になる。)
|
例:
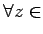
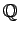
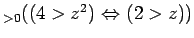 は正しい。
なぜなら、任意の正の有理数
は正しい。
なぜなら、任意の正の有理数 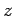 に対して、
だからである。
に対して、
だからである。
|
を証明するには、一つで良いから例をあげれば良い。
このときは、できるだけ具体的な例がよい。
|
例:
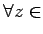
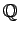
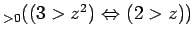 は正しくない。
すなわち、
である。なぜなら、正の有理数
は正しくない。
すなわち、
である。なぜなら、正の有理数 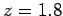 を考えると、
を考えると、
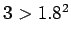 ではない(
ではない(
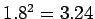 )のに
)のに 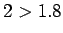 だからである。
だからである。
一般に、
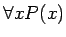 の否定は
の否定は
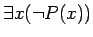 であり、
であり、
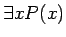 の否定は
の否定は
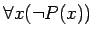 である。
したがって、例えば
である。
したがって、例えば
という具合に、
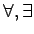 を含んだ命題の
否定は非常に簡単かつ形式的に得ることができる。
を含んだ命題の
否定は非常に簡単かつ形式的に得ることができる。
議論が複雑になってきたように感じられたら、 いったん記号で
主張を書いてみて整理するとわかりやすくなることが多い。
また、下の問題のように、幾つかに区切って考えるのも一法である。
その前に一つ注意をしておこう。
命題 5.1
一般に、正の実数
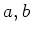
に対して
が成り立つのは
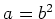
のときで、しかもそのときに限る。
平成19年11月29日
![]() の否定は
の否定は
![]() であり、
であり、
![]() の否定は
の否定は
![]() である。
したがって、例えば
である。
したがって、例えば