- 命題
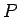 が正しい(真である)とき、その真理値は
が正しい(真である)とき、その真理値は 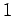 であると定める。
であると定める。
- 命題
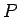 が正しくない(偽である)とき、その真理値は 0
であると定める。
が正しくない(偽である)とき、その真理値は 0
であると定める。
数学では、 幾つかの、真なる命題(公理)から出発して、 一定の推論規則を使って他の命題(補題や定理)を 導き出す。
(推論規則は、大変易しいが、ときとして日常での推論とは ずれることがある。これは主として、日常生活ではよく行なわれる 「含意」とか「行間を読む」といったものを数学では極力排していることによる。 すなわち、正しい証明を読めば(間違わない限りは、) 誰でも同じ結論にたどり着けるようにしてある。)
既存の命題から、新しい命題を生み出すための基本的な道具が、 「and, or, not」である。その説明のために、まず つぎの定義をしておく。
上の三つは、数学の推論の仕方の基本的な取り決めである。 「or」と「ならば」の使い方はとくに注意が必要である。 日常語としては、これらの語を上記以外の使い方で用いることもあるが、 「議論を明確にする」ために上のようにきめてあるわけだ。
かけ算における九九の表や、筆算のように、 真理値についても表をつくって理解の 助けにすることがある。これを真理表という。 形式は、どのようなものでも良いわけだが、例えばつぎのようにつくる。
| P | Q | P and Q | P or Q | not P | Q | (not P)or Q |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
上の表の一番右の欄が 「
![]() 」の真理値を表している。
」の真理値を表している。
| P | Q | P |
P and (P |
(P and (P |
| 0 | 0 | |||
| 0 | 1 | |||
| 1 | 0 | |||
| 1 | 1 |
「and, or , not ![]() 」 は日本語ではもちろん
それぞれ 「かつ、または、
」 は日本語ではもちろん
それぞれ 「かつ、または、![]() でない」である。
ここでは、強調のためあえて英語を用いた。
また、つぎのような記法が用いられることもある。
でない」である。
ここでは、強調のためあえて英語を用いた。
また、つぎのような記法が用いられることもある。