


Next: About this document ...
代数学演習 I 問題 No.1

定義 1.1
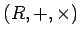
が環であるとは、それが次の3つの条件を満たすときに言います。
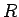 は
は 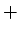 (加法) に関して加法群である。その単位元を 0
と書き、
(加法) に関して加法群である。その単位元を 0
と書き、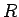 の零元と言います。
の零元と言います。
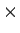 (乗法) は結合律を満たす。
(乗法) は結合律を満たす。
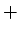 と
と 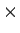 のあいだでは分配法則が成り立つ。すなわち、
のあいだでは分配法則が成り立つ。すなわち、
がすべての 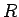 の元
の元 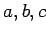 について成り立つ
について成り立つ
さらに
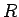
の元
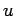
が
すべての $a&isin#in;R$ について
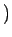
を満たすとき、
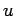
を
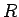
の単位元と言います。(普通は、単位元のことは
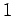
と書きます。)
簡単に言えば、普通の計算をやってると思って良いです。ただし、割り算ができないことと、積が可換とは限らないことが違います。また、乗法の 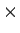 は省略することが多いです。例えば、
は省略することが多いです。例えば、
また、
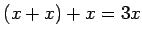 ,
,
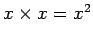 等と略記します。
等と略記します。
(演習の都合により、上の定義と今回(No.1)では、環の単位元の存在を仮定しません。
が、次回(No.2)からは、講義と歩調をあわせて、
環と言えば通常単位元をもつものとします。)
定義 1.2
積が可換である環を可換環と言います。単位元が存在して、
0
でない元で割り算ができるような可換環を体と言います。
問題 1.1
環
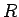
の元
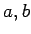
に対して、
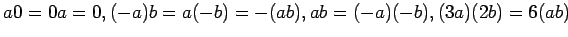
が成り立つことを示しなさい。 (
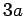
は
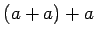
の略記であって、
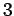
と
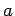
のかけ算では
ないことに注意。)
問題 1.2
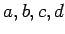
を 可換環 の元とするとき、次の式を展開しなさい。(全部で1)
問題 1.3
環の単位元は存在したとしてもただひとつであることを示しなさい。
(ヒント:
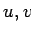
を二つの単位元とすると
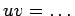
)
問題 1.4 (全部で1)
次の各集合は環でしょうか?
(加法、乗法は断らない限り自然なものを選ぶ。)
- 自然数全体の集合
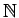
- 奇数全体の集合
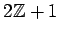
問題 1.6
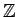
の部分集合であって、普通の足し算と掛け算について環になっているものを全て挙げなさい。
問題 1.7
実数の閉区間
![$ [0,1]$](img41.png)
上の連続関数全体は、適当な演算(各点ごとの足し算、掛け算)のもとに環になることを示しなさい。
問題 1.8
とおくと、
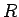
は各点ごとの足し算、掛け算によって環になることを示しなさい。
問題 1.9
前問の環
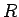
には単位元が存在しないことを示しなさい。



Next: About this document ...
2007-10-12
![]()
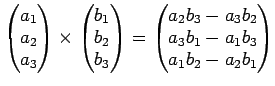 (ベクトルの外積)
(ベクトルの外積)