


Next: About this document ...
1=4
1 by -1
代数学 I No.4要約
 復習
復習
今日は復習と、定理や補題などの証明の
残していた部分を行う。そのあと、次のことについても
言及しよう。
例題 4.1
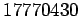
を
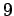
で割った余りを求めよ。
(解答)
整数 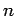 の
の
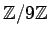 におけるクラス(剰余類)を
におけるクラス(剰余類)を 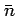 と書くことにする。
一般に、
と書くことにする。
一般に、
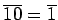 であることに注意すると、
であることに注意すると、
というという等式が成り立つことがわかる。これを用いると、
を得る。
(答え) 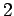
(注意)
九去算は計算機のない時代に、計算の確かめの目的で使われた。現在でも、
占い(バカラ占い)等で名残を見かけることがある。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
- あなたの思い付いた8桁以上の数(簡単すぎないもの)を
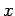 とします。
このとき、
とします。
このとき、
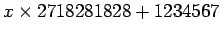 を9で割ったあまりを
(計算機やコンピュータを使わずに)
求めなさい。
を9で割ったあまりを
(計算機やコンピュータを使わずに)
求めなさい。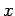 自身と、求め方も書くこと。なお、検算にコンピュータ等を
使用するのは構わないし、むしろ推奨する。
自身と、求め方も書くこと。なお、検算にコンピュータ等を
使用するのは構わないし、むしろ推奨する。
- (II).
-
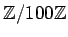 において、
において、
![$\displaystyle [x]_{100} \circ [y]_{100}=[$](img22.png)
($x$ を $y$ で割った余り)
![$\displaystyle ]_{100}
$](img23.png)
と「定義」する。
(ただし、![$ [x]_{100}$](img24.png) は整数
は整数 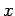 の
の
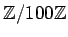 でのクラスとする。)
これは本当にうまく定義されているだろうか。
でのクラスとする。)
これは本当にうまく定義されているだろうか。
2007-10-23
![]() 復習
復習
![]()