![]()
三角関数, 指数関数, 対数関数等のいわゆる初等関数を 数学的に厳密に定義するためには、もうすこし準備を要する。 具体的には、角度、線分の長さ、面積の具体的な定義や、べき級数の とりあつかい等である。 ただ、これらの関数を全く知らないでいると不便なので、 ある程度厳密性を犠牲にして以下では概略を述べる。 高校までにならったことを思い出しておくとよい。
注意点: 角度は(とくに断らない限り)常に弧度法を用いる。
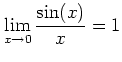
定義 5.1 の ![]() を思い出しておこう。
を思い出しておこう。
をみたすが、(広義でも狭義でも)単調増加ではないものの例をあげなさい。