


Next: About this document ...
数学概論1A要約 No.12
定義 12.1 (``教科書1.1.4'')
関数
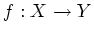
が
- 単射 であるとは、
言い換えると、
であるときにいう。
- 全射であるとは、
であるときにいう。
- 全単射であるとは、単射でかつ全射でもある時に言う。
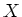 が弓の集合、
が弓の集合、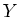 がトリの集合だとする。関数とは、
がトリの集合だとする。関数とは、
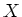 のおのおのからひとつづつ矢を発射、それぞれどれかの
トリに当てることを意味している。
のおのおのからひとつづつ矢を発射、それぞれどれかの
トリに当てることを意味している。
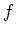 が単射であるとは、各々の矢がそれぞれ別のトリに
当たる(一つのトリに二つ以上の矢が当たることはない)と言う意味、
が単射であるとは、各々の矢がそれぞれ別のトリに
当たる(一つのトリに二つ以上の矢が当たることはない)と言う意味、
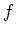 が全射であるとは、すべての矢がそこにいる全てのトリにあたる
という意味である。
が全射であるとは、すべての矢がそこにいる全てのトリにあたる
という意味である。
同じ式でも定義域 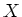 と 終域
と 終域 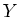 が何であるかによって、全射か単射かは
異なる。
次のことは、簡単だが大変重要である。
が何であるかによって、全射か単射かは
異なる。
次のことは、簡単だが大変重要である。
定理 12.1
- 関数
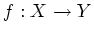 が全単射ならば、
が全単射ならば、 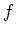 の逆写像が存在する。
の逆写像が存在する。
- 逆に 関数
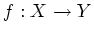 が逆写像を持つならば、
が逆写像を持つならば、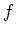 は全単射である。
は全単射である。
- 関数
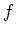 の逆写像は、存在すれば一意的である。
の逆写像は、存在すれば一意的である。
連続関数の場合はどうであろうか。一変数では関数の単調性がキーになる。
定義 12.2 (``1.3.6'')
実数のある区間
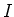
で定義された関数
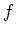
が狭義単調増加関数であるとは、
をみたすときにいう。
定理 12.2 (``教科書定理1.16'')
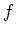
が閉区間
![$ [a,b]$](img11.png)
上の狭義単調増加な連続関数であれば、
の逆関数
が存在する。
さらに、この
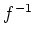
は連続で、かつ狭義単調増加である。
問題 12.1
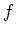
は閉区間
![$ [0,1] $](img15.png)
上の実数値連続関数 (
![$ f:[0,1]\to$](img16.png)
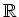
) で、
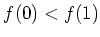
であるとする。
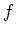
が単射ならば、
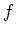
は狭義単調増加でなければ
ならないことを証明しなさい。
話は全然違うが、時間が許せば次のことも証明しておこう。
(使うのは二学期の積分論のとき。)
定理 12.3
閉区間
![$ [a,b]$](img11.png)
上の連続関数
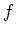
は
一様連続である。すなわち
がなりたつ。
2007-07-04
![]()
![]() が弓の集合、
が弓の集合、![]() がトリの集合だとする。関数とは、
がトリの集合だとする。関数とは、
![]() のおのおのからひとつづつ矢を発射、それぞれどれかの
トリに当てることを意味している。
のおのおのからひとつづつ矢を発射、それぞれどれかの
トリに当てることを意味している。
![]() が単射であるとは、各々の矢がそれぞれ別のトリに
当たる(一つのトリに二つ以上の矢が当たることはない)と言う意味、
が単射であるとは、各々の矢がそれぞれ別のトリに
当たる(一つのトリに二つ以上の矢が当たることはない)と言う意味、
![]() が全射であるとは、すべての矢がそこにいる全てのトリにあたる
という意味である。
が全射であるとは、すべての矢がそこにいる全てのトリにあたる
という意味である。
![]() と 終域
と 終域 ![]() が何であるかによって、全射か単射かは
異なる。
次のことは、簡単だが大変重要である。
が何であるかによって、全射か単射かは
異なる。
次のことは、簡単だが大変重要である。