![]()
がなりたつとすると、
がそれぞれ存在するとする。このとき、
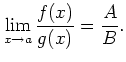
をみたすような正の数
であることを示しなさい。
|
|
をみたせば、![]() は
は ![]() で連続であると言えるだろうか、
理由を挙げて述べなさい。(少しむずかしい)
で連続であると言えるだろうか、
理由を挙げて述べなさい。(少しむずかしい)
![]() のいろいろな
のいろいろな ![]() についての値
についての値
|
|
|||
| 1 | 1 | 1.10 | 0.909 |
| 2 | 32 | 1.21 | 26.446 |
| 3 | 243 | 1.33 | 182.569 |
| 10 | 100000 | 2.59 | 38554.329 |
| 51 | 345025251 | 12912 | 2671922.994 |
| 52 | 380204032 | 14204 | 2676683.920 |
| 53 | 418195493 | 15624 | 2676498.687 |
| 100 | 10000000000 | 13780.61 | 725657.159 |
| 200 | 320000000000 | 189905276.53 | 1685.051 |
| 299 | 2389769101499 | 2379100905625.82 | 1.004 |
| 300 | 2430000000000 | 2617010996188.40 | 0.928 |
| 310 | 2862915100000 | 6787852539362.45 | 0.422 |
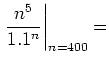 |
0 | |||
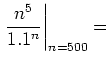 |
0 |
![\includegraphics[scale=0.5]{n5_11n.ps}](img48.png)