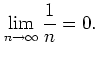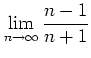Next: About this document ...
数学概論1A要約 No.3
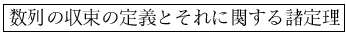
収束の定義は前回の定義 2.4で述べた通りである。
それでは定義 2.4 の判定法を満たす 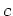 は唯一つだろうか?
は唯一つだろうか?
定理 3.1
数列
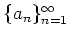 が
が(
ある人が確かめたところ)
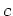 に収束し、
に収束し、
(
別の人が確かめたところ)
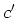 にも収束するなら、
にも収束するなら、
である。つまり、数列の収束先は存在するとしたら唯一つしかない。
そこで、つぎのように定義することができる。
定義 3.1
数列
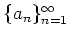
がある数
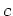
に収束するとき、
と書いて、
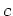
のことを
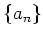
の
極限と呼ぶ。
定義のあとは、これに慣れるためにいくつか練習を行なう。
まずは、例である。
厳密には、上の例の証明には次のようなことを使う。
補題 3.1
任意の実数 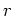 に対して、それよりも大きな整数
に対して、それよりも大きな整数 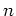 が存在する。
が存在する。
さて、つぎには極限のもつ一般的な性質について知らねばならない。
次のような事実が基本的である。
定理 3.2
極限をとるという操作は和、差、積、商、大小関係を保存する。
具体的な意味はテキストの``定理1.4'' と``定理1.2''を参照のこと。
このような定理に厳密な証明をつけ得ることが定義 2.4 の良いところである。
問題 3.1
を求め、その答が
確かに正しいことを
定義 2.4 で述べた定義に基づいて
証明せよ。
2007-05-02
![]()
![]() は唯一つだろうか?
は唯一つだろうか?