


Next: About this document ...
日本語技法 No.6
集合算
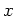 についての命題
についての命題 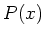 と
と
を対応づけると、命題の議論を集合の議論に置き換えられることがある。
それ以外にも、命題と集合とのあいだには密接な関係がある。
集合の包含関係
集合を扱うときに、例えば、
はそれぞれ違うものである。明確に区別する必要がある。
集合と写像を組み合わせた問題は、論理力をみがく格好の材料である。
定義 6.1
写像
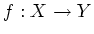
が与えられているとき、
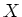 の部分集合
の部分集合 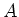 に対して
に対して
を 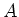 の
の 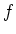 による像といい、
による像といい、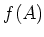 で表す。
で表す。
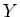 の部分集合
の部分集合 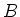 に対して
に対して
を 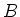 の
の 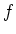 による逆像といい、
による逆像といい、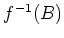 で表す。
で表す。
レポート解答における注意事項
- すでに証明された結果(...である。)と、
これから証明すべき結果(...を証明しよう。)、
仮定(...を仮定する)の区別が明確になるように書くこと。
- 図やグラフを描いた場合、そのどの部分に着目するかを必ず書くこと。
問題 6.1
定義
6.1 の状況の下で、
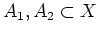
,
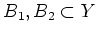
とするとき、
はいつでも正しいだろうか。正しい場合には証明し、
正しくない場合には具体的な反例を挙げよ。
面白いことに、写像を扱う上では、
「像」よりも「逆像」のほうが楽な場合が多い。
たとえば、「逆像をとる」という操作は
集合の和、共通部分を考える操作など多くの操作と可換である。
2006-11-22
![]() についての命題
についての命題 ![]() と
と