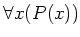日本語技法 No.4

$\forall$ と $\exists$

定義 4.1   変数 $x$ を含むような命題 $P$ にたいして、

1. $\forall x (P(x))$ は 「どのような 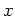$x$ にたいしても、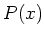$P(x)$ が成り立つ」 という意味である。
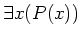2. $\exists x (P(x))$ は 「少なくとも一つの 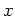$x$ にたいして、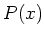$P(x)$ が成り立つ」 という意味である。

原理的には、$\forall$ , $\exists$ および前回の論理記号と、 集合論の幾つかの記号を組み合わせることにより、数学の すべての言葉を記号列に翻訳できる。

例えばつぎの文は、「数学的帰納法」を表現したものである。

$$\forall S(0\in S$$ and $$(\forall n\in\mathbb{N}(n\in S\implies (n+1)\in S)) \implies \mathbb{N}\subset S)$$

また、つぎの文章は、「 $(X,\mathcal U)$ は位相空間である」 ということ(の定義)を述べたものである。

1. $\mathcal U \subset 2^X.$
2. $(\emptyset \in \mathcal U )$    and $(X\in \mathcal U).$
3. $\forall U( \forall V(U,V\in \mathcal U \implies U\cap V \in \mathcal U)).$
4. $\forall \mathcal S (\mathcal S\subset \mathcal U \implies \bigcap_{ U\in \mathcal S } U\in \mathcal U).$

数学における論理は、 これらの記号列に関する「単純な計算」である。 つまり、「論理を追う」とは、これらの単純な計算を 間違いなく素早く行なうことである。それは、 かけ算の九九と同じように、 練習をすればほとんど誰でもできる。 ただし、つぎのような練習が必要である。

1. 計算法を覚えること。
2. 時おり計算の意味を考えること。
3. 発展問題について解いてみること。

さしあたって今回は、つぎのことに注意しよう。

登場人物($x$ や $y$ などの変数)の出てくる順番が 大事である。

例えば、 $J=\{$グー、チョキ、パー$\}$ , にたいして、 $x\succ y$ を、「$x$ は $y$ より強い」というふうに定義すると。

$$\forall x\in J (\exists y\in J ( y \succ x))$$

は真の命題だが、

$$\exists y\in J (\forall x\in J( y \succ x))$$

は偽の命題である。

問題 4.1   変数 $x,y$ についての命題 $P(x,y)$ で、

$$\forall x \exists y (P( x , y))$$

は真の命題だが、

$$\exists y \forall x( P(x, y))$$

は偽の命題である ようなものを挙げ、どうしてそうなのか解説を書きなさい。

&dotfill#dotfill;

(補遺)

$$\forall x\in J (P(x))$$

はきちんと書くと

$$\forall x (x\in J \implies P(x))$$

という意味、

$$\exists y\in J (P(y))$$

はきちんと書くと

$$\exists y (y\in J$$    and $$P(y))$$

という意味の省略形である。