DEFINITION 5.56
Let
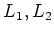
be Lie algebras over a commutative ring
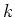
.
we say ``
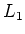 acts on
acts on 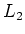 as a derivation
as a derivation'' if
there is given a Lie algebra homomorphism
If the action
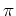
is obvious in context,
we shall simply denote
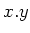
instead of
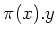
.
DEFINITION 5.57
Let
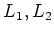
be Lie algebras over a commutative ring
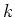
.
Assume there is given an action
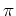
of
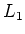
on
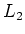
.
Then we define a
semi direct product
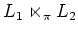
of
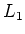
and
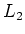
by
introducing the
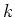
-module
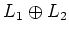
with
the following bracket product.
Note that
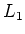 and
and 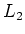 are (identified with) subalgebras of
are (identified with) subalgebras of
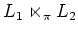 .
.
- Further more,
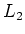 is an ideal of
is an ideal of
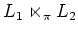 .
.
- For
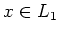 and
and 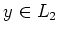 , we have
, we have
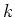 -linear) derivation of
-linear) derivation of 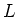 is a
is a 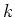 -linear map
-linear map 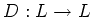 such that it obeys the following ``Leibniz rule''.
such that it obeys the following ``Leibniz rule''.
![$\displaystyle D([x,y])=[D x,y]+ [x, D y] \qquad (\forall x,y\in L).
$](img625.png)
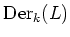 the set of all derivations of
the set of all derivations of 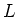 .
.