PROOF..
Since
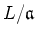
is solvable,
there exists a positive integer
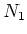
such that
Then we obviously have
On the other hand, since
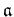
is solvable,
there exists a positive integer
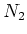
such that
We thus have
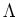
PROOF..
Let
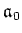
be a solvable ideal of
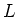
which has the maximal dimension among
solvable ideals. Then for any solvable ideal
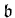
of
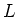
,
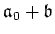
is also solvable. Thus by the choice of
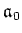
we see that
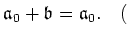
That is,
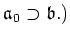
Thus we see that
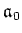
is the largest solvable ideal of
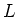
.
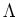
![]()
![]()
![]() contains
contains