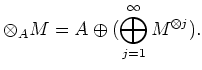

Next: exterior derivation
Up: Topics in Non commutative
Previous: functoriality
Let 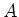 be a commutative algebra.
Let
be a commutative algebra.
Let 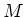 be an
be an 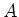 -module.
-module.
The tensor algebra
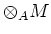 is defined as
is defined as
It is a (non commutative)
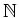 -graded algebra
1 over
-graded algebra
1 over 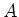 .
Let us define the following two sided ideal of
.
Let us define the following two sided ideal of
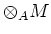 .
.
Then we define
2007-12-26
![]() is defined as
is defined as