

Next: Relations of derivations.
Up: some linear algebra
Previous: interior derivation
Lie derivation appears in a wide contexts.
It is based on the following observation.
Let 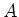 be a commutative ring. Let
be a commutative ring. Let 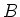 be a commutative
be a commutative 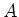 -algebra.
Let
-algebra.
Let 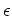 be the dual number.
be the dual number.
Then for any
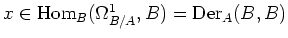 , we define
, we define
It is an
 -algebra automorphism of
-algebra automorphism of
 which
reduces to the identity when we put
which
reduces to the identity when we put
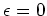 .
So any natural construction on algebras may be transformed by
this map. Among such constructions is the modules of differential forms,
modules of derivations, tensor products of them, and the dual of them.
.
So any natural construction on algebras may be transformed by
this map. Among such constructions is the modules of differential forms,
modules of derivations, tensor products of them, and the dual of them.
We may also introduce
to be the unique 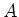 -linear map which satisfies the following properties.
-linear map which satisfies the following properties.
-
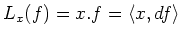 for any
for any 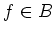 .
.
-
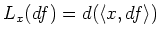 for any
for any 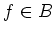 .
.
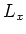 is an even derivation. That means,
is an even derivation. That means,
Other useful Lie derivation is that for vector fields. Namely, Let 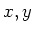 be two
be two 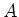 -derivations from
-derivations from 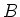 to
to 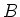 . Then we define
. Then we define
Lie derivations commute with contractions. Namely,
We leave it the reader to do the detailed discussion.


Next: Relations of derivations.
Up: some linear algebra
Previous: interior derivation
2007-12-26
![]() be two
be two ![]() -derivations from
-derivations from ![]() to
to ![]() . Then we define
. Then we define