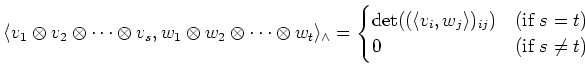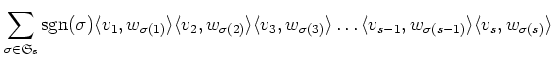

Next: interior derivation
Up: some linear algebra
Previous: even and odd derivations.
Let 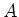 be a commutative ring. Let
be a commutative ring. Let 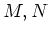 be
be 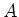 -modules.
Assume there is a
-modules.
Assume there is a 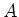 -bi-linear pairing
-bi-linear pairing
Then we define a pairing of tensor algebras
defined by the following equation.
(The reader may prefer the expression
rather than the expression above which uses a determinant.)
Then it is easy to see that the pairing above descends to define a
pairing of exterior algebras
2007-12-26