

Next: fiber product
Up: Elementary category theory
Previous: universe
In this section we fix a sufficiently large universe 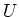 .
For some of readers it may be happier to neglect the term ``U-small''.
.
For some of readers it may be happier to neglect the term ``U-small''.
EXAMPLE 5.5
The category

of
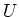
-small sets.
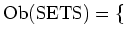
$U$-small sets
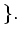
For any
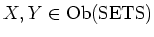
, we put
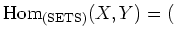
the set of all maps from $X$ to $Y$.
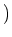
EXAMPLE 5.6
The category
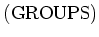
of
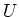
-small groups (that means, groups that are
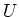
-small as sets).
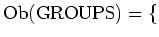
$U$-small groups
For any
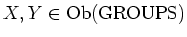
, we put
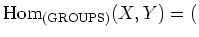
the set of all group homomorphisms from $X$ to $Y$.
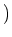
Likewise, we may easily define categories such as the category
 of
of 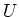 -small-rings, the category
-small-rings, the category
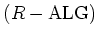 of algebras over
a ring
of algebras over
a ring 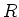 , the category
, the category
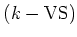 of
of
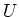 -small vector spaces over a field
-small vector spaces over a field 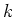 , and so on.
, and so on.
EXAMPLE 5.7
The category
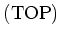
of
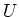
-small topological space
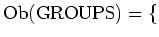
$U$-small topological space
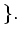
For any
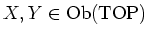
, we put
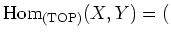
the set of all continuous maps from $X$ to $Y$.
One may also consider
the category of 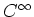 -manifolds, the category of
-manifolds, the category of 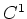 -manifolds,
and so on.
-manifolds,
and so on.
Of course, the category of schemes (with morphisms the ones we defined in the
previous part) is very important category for us.


Next: fiber product
Up: Elementary category theory
Previous: universe
2007-12-11
![]() of
of ![]() -small-rings, the category
-small-rings, the category
![]() of algebras over
a ring
of algebras over
a ring ![]() , the category
, the category
![]() of
of
![]() -small vector spaces over a field
-small vector spaces over a field ![]() , and so on.
, and so on.
![]() -manifolds, the category of
-manifolds, the category of ![]() -manifolds,
and so on.
-manifolds,
and so on.