Smooth morphism

For any non negative integer 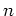$n$ and for any scheme 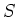$S$ , we put

$$\mathbb{A}^n_S=\operatorname{Spec}\mathbb{Z}[x_1,x_2,\dots,x_n] \times_{\operatorname{Spec}\mathbb{Z}} S$$

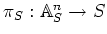and $\pi_S:\mathbb{A}^n_S\to S$ the standard projection.

A smooth scheme over 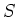$S$ is a scheme which ''étale locally look like'' $\mathbb{A}^n_S$ .

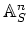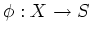
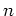
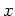
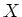
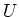
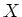
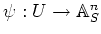
DEFINITION 10.7   A separated morphism $\phi:X\to S$ of finite type is smooth of relative dimension $n$ if for any point $x$ on $X$ , there exists an open neighborhood $U$ of $X$ and an 'etale morphism $\psi: U\to \mathbb{A}^n_S$ such that

$$\phi =\psi \circ \pi_S$$

holds.

Let us close this section by quoting the following fundamental result.

THEOREM 10.8 (SGA1,Éxpose II,Corollary4.6)   Let $f:X\to Y$ be a morphism of smooth $S$ -schemes. then $f$ is étale at $x\in X$ if and only if $f^*(\Omega^1_{Y/S}) \to \Omega^1_{X/S}$ is isomorphism at $x$ .