Benefit of being a sheaf.

By saying that $\mathcal{O}$ is a sheaf on $\operatorname{Spec}(A)$ , we may easily use the arguments we have used to proved the locality and the gluing lemma.

For example, the proof we gave in Theorem 1.16, especially the part where we chose the idempotent $p_1$ , was a bit complicated.

Let us give another proof using the sheaf arguments. There exists a unique element $p\in A=\mathcal{O}(\operatorname{Spec}(A))$ which coincides with $1$ on $U_1=V(J)$ and with 0 on $U_2=V(I)$ . From the uniqueness we see that

$$p^2=p$$

holds since $p^2$ satisfies the same properties as $p$ . The rest of the proof is the same.

As a second easier example, we consider the following undergraduate problem.

Problem: Find the inverse of the matrix

$$\begin{pmatrix} 3& 5 \\ 1 & 2 \end{pmatrix}.$$

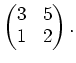
A student may compute (using ``operations on rows'') as follows.

$$\begin{pmatrix}3& 5 &\vert & 1 &0 1 & 2 &\vert & 0 & 1 \end{pma... ... \to \begin{pmatrix}1& 5/3 &\vert & 1/3 &0 1 & 2 &\vert & 0 & 1 \end{pmatrix}$$

$$\to \begin{pmatrix}1& 5/3 &\vert & 1/3 &0 0 & 1/3 &\vert & -1/3 & 1... ...\to \begin{pmatrix}1& 5/3 &\vert & 1/3 &0 0 & 1 &\vert & -1 & 3 \end{pmatrix}$$

$$\to \begin{pmatrix}1& 0 &\vert & 2 &-5 0 & 1 &\vert & -1 & 3 \end{pmatrix}$$

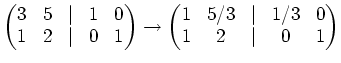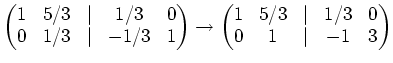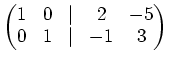The calculation is valid on $\operatorname{Spec}(\mathbb{Z}[1/3])$ .

Another student may calculate (using ``operations on columns'') as follows.

$$\begin{pmatrix}3& 5 &\vert & 1 &0 1 & 2 &\vert & 0 & 1 \end{pma... ... \to \begin{pmatrix}3& 5/2 &\vert & 1 &0 1 & 1 &\vert & 0 & 1/2 \end{pmatrix}$$

$$\to \begin{pmatrix}1/2& 5/2 &\vert & 1 &0 0 & 1 &\vert & -1/2 & 1/2... ...\to \begin{pmatrix}1& 5/2 &\vert & 2 &0 0 & 1 &\vert & -1 & 1/2 \end{pmatrix}$$

$$\to \begin{pmatrix}1& 1 &\vert & 2 &-5 0 & 1 &\vert & -1 & 3 \end{pmatrix}$$

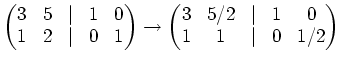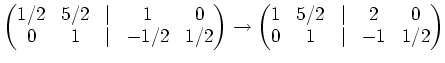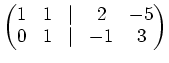The calculation is valid on $\operatorname{Spec}(\mathbb{Z}[1/2])$ . Of course, both calculations are valid on the intersection $\operatorname{Spec}(\mathbb{Z}[1/2])\cap \operatorname{Spec}(\mathbb{Z}[1/3])=\operatorname{Spec}(\mathbb{Z}[1/6])$ .

The gluing lemma asserts that the answer obtained individually is automatically an answer on the whole of $\operatorname{Spec}(\mathbb{Z})$ . Of course, in this special case, there are lots of easier ways to tell that. But one may imagine this kind of thing is helpful when we deal with more complicated objects.