![]() ユークリッドの互除法
ユークリッドの互除法
(解答)
同様に、
さて、
![]() とおき、
とおき、![]() が
が ![]() とは
異なるとしてみる。上と全く同じ操作を行なうと、
とは
異なるとしてみる。上と全く同じ操作を行なうと、
このことから
を得る。逆に、この等式さえ知っておれば、上の例題に対する一行の解答が
と言う具合に書ける。
このような計算を容易に行なうのがユークリッドの互除法である。 ここでは手っ取り早く、つぎのような行列算を使う方法を紹介する。
を満たす整数
(解答) まず次のような計算を行なう
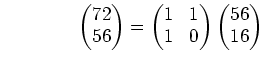 |
||||||||||||
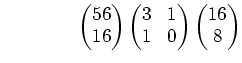 |
||||||||||||
| 0 | 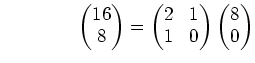 |
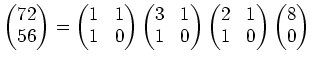
を得る。この式の右辺に現れる正方行列はすべて
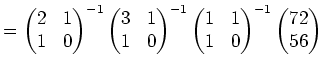 |
||
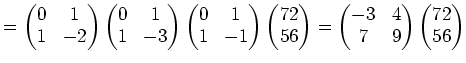 |
(答)
![]() .
.
※レポート問題
の形で書きなさい。 (