1=3     

代数学 C(コア) 演習問題 No.3

部分群

群の部分群とは、部分集合であって群になっているもののことです。

ただし、部分群の掛け算はもとの群の掛け算と一致しなければなりません。 部分群の正確な定義は次のようになります。

定義 3.1 (部分群の定義)  

群 $(G,m)$ が与えられているとします。 $G$ の部分集合 $H$ が $G$ の部分群であるとは 、次の条件を満たすときに言います。

(0)掛け算 $m:G\times G\to G$ を $H\times H$ に制限すると、 これは $H$ に値を持つ。すなわち、次のような写像が誘導される。

$$m:H\times H \to H$$

(1) $(H,m)$ は 群である。

条件 (0) は次のように言い換えても良い。

(0$'$ ) $h,k$ を $H$ から任意に取ってくると、 いつでも $m(h,k)$ は $H$ の元である。

問題 3.1   次の集合は整数の加法群 $({\mbox{${\mathbb{Z}}$}},+)$ の部分群をなしますか? 理由をつけて答えなさい。

1. $(1/2){\mbox{${\mathbb{Z}}$}}$ = $\{0,1/2,-1/2,1,-1,3/2,-3/2,\dots\}$ .
2. $\{\pm 1 \}$ .
3. 0 以上の整数の集合 $\mathbb{N}=\{0,1,2,3,4,\dots,\}$ .
4. $7$ で割って $1$ 余る整数全体の集合 $7{\mbox{${\mathbb{Z}}$}}+1$ .
5. $4$ で割り切れる整数全体の集合 $4{\mbox{${\mathbb{Z}}$}}$ .

問題 3.2 (10点)   次の集合は有理数全体のなす加法群 ( ${\mathbb{Q}}$ ,+) の部分群をなしますか? 理由をつけて答えなさい。

1. $(1/2){\mbox{${\mathbb{Z}}$}}$ = $\{0,1/2,-1/2,1,-1,3/2,-3/2,\dots\}$ .
2. 実数全体の集合 $\mbox{${\mathbb{R}}$}$ .
3. $7$ で割って $1$ 余る整数全体の集合 $7{\mbox{${\mathbb{Z}}$}}+1$ .
4. 0 以外の有理数全体が通常の掛け算についてなす群 $($$\mbox{${\mathbb{Q}}$}$$^{\times},\times)$ .

問題 3.3   $({\mbox{${\mathbb{Z}}$}},+)$ の部分群 $H$ が $6$ を元として含めば、

1. $12$ も $H$ の元であることを示しなさい。
2. $108$ も $H$ の元であることを示しなさい。
3. $-216$ も $H$ の元であることを示しなさい。
4. $6$ の倍数全体 $6{\mbox{${\mathbb{Z}}$}}$ は $H$ の部分集合であることを示しなさい。

問題 3.4   $({\mbox{${\mathbb{Z}}$}},+)$ の部分群 $H$ が $200$ と $55$ を元として含むということを 知っていたとします。このとき。

1. $55\times 3(=165)$ も $H$ の元であることを示しなさい。
2. $200-165(=35)$ も $H$ の元であることを示しなさい。
3. $H$ に確実にはいっているといえる 正の整数のうち、最小のものは何ですか？

問題 3.5   0 以外の有理数のなす乗法群 $($$\mbox{${\mathbb{Q}}$}$$^{\times},\times)$ の部分群 $H$ が $2$ を元として含んでいたとします。このとき、「$H$ の正の元のうち最小のもの」は 存在しないことを示しなさい。

問題 3.6   整数全体のなす加法群 $G=({\mbox{${\mathbb{Z}}$}},+)$ を考えます。

1. 整数 $n$ を一つ決めると、$G$ の部分集合 $n{\mbox{${\mathbb{Z}}$}}$ が、
   $$n{\mbox{${\mathbb{Z}}$}}= \{n m; m\in {\mbox{${\mathbb{Z}}$}}\}$$
   によって決まりますが、これは $G$ の部分群であることを示しなさい。
2. 逆に、$G$ の部分群 $H$ は必ず (1) の形で書けることを示しなさい。 (ヒント：$H$ の元のうち、正で、最小なものを $n$ としてみなさい。)

問題 3.7   実数を成分にもつ2次の正則行列の全体は掛け算に関して群をなします。 (証明不要) これを普通 ${\operatorname{GL}}_2($$\mbox{${\mathbb{R}}$}$$)$ と書きます。さて、

$$A= \begin{pmatrix} 5 & 3 \\ -7 & -4 \end{pmatrix}$$

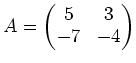
を含む ${\operatorname{GL}}_2($$\mbox{${\mathbb{R}}$}$$)$ の部分群で、 ${\operatorname{GL}}_2($$\mbox{${\mathbb{R}}$}$$)$ 自身とは異なるものの例を 一つあげなさい。

つぎの諸問題は本に載っているかも知れないけれども、 それを丸うつしにしても点数は与えません。 今回の冒頭に述べた定義3.1から出発して以下のの事実が 論理的な飛躍なしに 説明できるかどうかがポイントです。

問題 3.8  

1. $H$ と $K$ が、ともに群 $G$ の部分群であれば、 $H\cap K$ も $G$ の部分群となることを示しなさい。
2. ${\mbox{${\mathbb{Z}}$}}$ の部分群 $H,K$ で、$H\cup K$ が ${\mbox{${\mathbb{Z}}$}}$ の部分群に ならない例を一つあげなさい。

問題 3.9   ${\mbox{${\mathbb{Z}}$}}$ の部分群 $H=m{\mbox{${\mathbb{Z}}$}}$ と $K=n{\mbox{${\mathbb{Z}}$}}$ との共通部分 $H\cap K$ を求めなさい。

問題 3.10   $H$ が群 $G$ の部分群であれば、$G$ のどの元 $t$ についても、 $tHt^{-1}$ は $G$ の部分群となることを示しなさい。

問題 3.11   群 $G$ の部分群 $H,K$ について、集合 $HK$ も部分群となるための必要十分条件は、 $KH=HK$ が成立することである事を示しなさい。