o) まずは ![]() (単位行列)にとる。必然的にこのとき
(単位行列)にとる。必然的にこのとき ![]() ,
, ![]() である。
である。
(計算):次の i),ii) を繰り返す
i) ![]() =0 なら (仕上げ) に進む。
=0 なら (仕上げ) に進む。
ii) ![]() を
を ![]() で割った商を
で割った商を ![]() , 余りを
, 余りを ![]() とおくと、
とおくと、
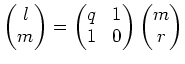
なる関係に着目する。右辺にでてくる二次行列の逆行列は 直ちに計算できて、
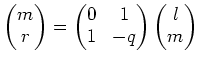
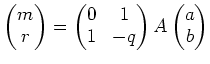
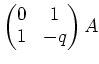
(仕上げ)さて、 ![]() になったはずである。 このとき、
になったはずである。 このとき、
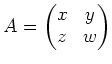
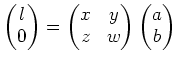
| (I) |
他方、
![]() に注意すると、
に注意すると、
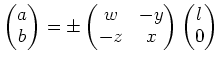
(II) ![]() は
は ![]() の倍数である。
の倍数である。
(I),(II) をあわせると、![]() は
は ![]() の最大公約数
の最大公約数 ![]() と
等しくなければならないことが分かる。
と
等しくなければならないことが分かる。
すなわち、(仕上げ)まですすんだところで ![]() の成分の
の成分の ![]() と、
と、
![]() が求めるものになる。
が求めるものになる。