


: この文書について...
代数学 I No.10要約
 《単項イデアル整域は素元分解環である》
《単項イデアル整域は素元分解環である》
今回は、単項イデアル整域(単項イデアル環で、整域にもなっているもの、
略してPID)は、
「素因数分解」が出来ることをしめす。
まず、
のような無用の分解を避けるために、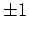 に類するものを特別扱いする
ことにする。
に類するものを特別扱いする
ことにする。
定義 10.1
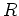
は環であるとする。
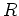
の元のうち、
積に関して可逆なものの全体を
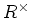
であらわす。
補題 10.1
可換環
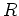
の元
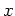
について、次は同値である。
-
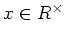
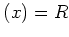
定義 10.2
可換環
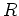
の元
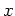
が素元であるとは、
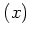
が
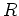
の素イデアルであるときにいう。
例えば、
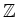 ,
,
![$ {\mathbb{C}}[X]$](img17.png) は素元分解環である。もっと一般に、
次のことが成り立つ。
は素元分解環である。もっと一般に、
次のことが成り立つ。
定理 10.1
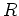
が単項イデアル整域ならば、
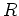
は素元分解環である。
この定理の証明はいくつかの段階にわかれる。
まず、次の事実の拡張からはじめよう。
事実 10.1
整数
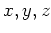
があって、
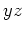
は
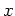
で割り切れ、
かつ
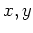
が互いに素であるとする。このとき、
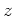
は
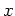
で割り切れる。
整数 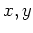 が互いに素なら、
が互いに素なら、
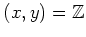 であったことを思い起こすと、
次の補題は上の事実の拡張であることが分かるだろう。
であったことを思い起こすと、
次の補題は上の事実の拡張であることが分かるだろう。
補題 10.2
可換環
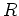
の元
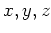
があって、
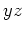
は
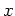
で割り切れ、かつ
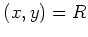
であるとする。このとき、
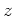
は
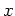
で割り切れる。
定義 10.4
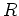
は可換環であるとする。
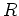
の元
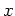
が既約であるとは、
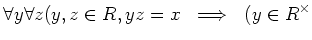
または
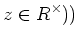
のときに言う。
上の補題により、単項イデアル整域 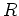 の元
の元 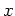 を素因数分解する手順は
次のようになる。
を素因数分解する手順は
次のようになる。
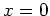 または
または
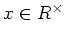 ならば、おしまい。
ならば、おしまい。
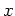 が素元ならば、やはりおしまい。
が素元ならば、やはりおしまい。
- それ以外なら、
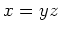 (
(
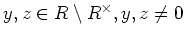 )と
分解できる。
)と
分解できる。
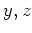 について同様のことをする。
(例えば
について同様のことをする。
(例えば 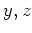 が 素元でなければ、
が 素元でなければ、 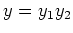 となる。)
となる。)
- 繰り返す。
あとの問題は、一つの元が無限に分解されていかないか、ということである。
これを解決するのには、前回の補題を用いればよい。
(参考)
![$ {\mathbb{C}}[X]$](img17.png) の部分環
の部分環
![$ R={\mathbb{C}}[X^2,X^3]$](img31.png) を考えると、
を考えると、
![$\displaystyle R=\{f\in {\mathbb{C}}[X];$](img32.png)
$f$ の $X$ に関する一次の項の係数は $0$
であることが分かる。ここで、
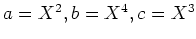 とおくと、
とおくと、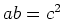 であるが、
であるが、
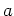 は
は 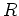 のなかで既約である
のなかで既約である
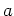 は
は 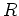 のなかで
のなかで 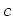 の約数ではない。
の約数ではない。
ということが分かる。このように、単に「環」といってもこのような「特異な」環も
含まれるので、その元の取り扱いには通常の整数を取り扱う以上の注意が必要である。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
- 整域
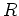 に対して、次のことを示しなさい。
に対して、次のことを示しなさい。
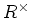 は乗法に関して群をなす。
は乗法に関して群をなす。
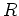 に次のような同値関係をいれることが出来る。
(この同値関係で同値な二つの元を、同伴な二つの元と呼ぶ。)
に次のような同値関係をいれることが出来る。
(この同値関係で同値な二つの元を、同伴な二つの元と呼ぶ。)
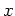 が
が 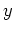 の倍元で、
の倍元で、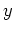 が
が 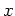 の倍元でもあるなら、
の倍元でもあるなら、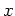 と
と 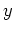 とは
同伴である。
とは
同伴である。
- (II).
- 整域
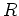 が与えられているとし、
が与えられているとし、
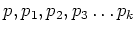 は全て
は全て 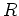 の素元であるとする。このとき、もし
の素元であるとする。このとき、もし
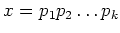 が
が
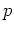 の倍元であれば、
の倍元であれば、
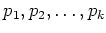 のうちどれか一つは必ず
のうちどれか一つは必ず
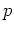 と同伴であることを示しなさい。(同伴の定義は前問参照。但し、
前問に答えることは要求しない。(前問の結果は仮定してよい。))
と同伴であることを示しなさい。(同伴の定義は前問参照。但し、
前問に答えることは要求しない。(前問の結果は仮定してよい。))
- (III).
-
![% latex2html id marker 1169
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{-1}]$](img45.png) はユークリッド環、したがって素元分解環である。(証明不要)
そこで、
はユークリッド環、したがって素元分解環である。(証明不要)
そこで、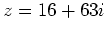 を
を
![% latex2html id marker 1173
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{-1}]$](img47.png) において素元分解せよ。
(ヒント: まず
において素元分解せよ。
(ヒント: まず 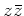 の素因数分解を試みよ。素因数分解の一意性を信じれば、
いろんな数の共通因数が求めたくなる筈である。
そういうときはユークリッドの互除法を用いよ。最後に、
数が本当に素元であるかどうか知りたいときには、
の素因数分解を試みよ。素因数分解の一意性を信じれば、
いろんな数の共通因数が求めたくなる筈である。
そういうときはユークリッドの互除法を用いよ。最後に、
数が本当に素元であるかどうか知りたいときには、
ということをうまく用いよ。
)



: この文書について...
平成17年12月19日
![]() 《単項イデアル整域は素元分解環である》
《単項イデアル整域は素元分解環である》
![]() ,
,
![]() は素元分解環である。もっと一般に、
次のことが成り立つ。
は素元分解環である。もっと一般に、
次のことが成り立つ。
![]() の元
の元 ![]() を素因数分解する手順は
次のようになる。
を素因数分解する手順は
次のようになる。
![]() の部分環
の部分環
![]() を考えると、
を考えると、