


: この文書について...
代数学 I No.9要約
《ユークリッド環は単項イデアル環であること》
前回、次の定理およびその周辺が
残っていたので、今回はその解説である。
定理 9.1
ユークリッド環は単項イデアル環である。
次回の準備のために、次のことも証明しておこう。
補題 9.1
単項イデアル環
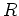
のイデアルの増大列
は必ずどこかで止まる。すなわちある
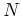
があって、
がなりたつ。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
-
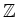 のイデアルの減少列
の例をあげなさい。
のイデアルの減少列
の例をあげなさい。
平成17年12月11日
![]()